---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
# [ source("http://macosa.dima.unige.it/r.R") ]
# We refer to the introduction to R language here, here and here for the bases.
# We refer to WikiPedia (the English version only!) to go deep into Statistics
# ---------- ---------- ---------- ----------
# To have numerical indicators of asimmetry (skewness) of a data distribution see here.
# ---------- ---------- ---------- ----------
# What does "to take randomly" mean? It depends on the law of distribution with which
# it is done. Two processes that generate a point falling into the circle with center O
# and radius 1 and test if its distance from O is less than 1/2.
BF=3;HF=3; BOXW(-1,1, -1,1)
circle(0,0, 1, "brown"); circle(0,0, 1/2, "brown"); BOX()
type(-1,1,"-1"); type(1,1,"1"); type(-1,-1,"-1"); type(1,-1,"1")
n = 0; ok = 0; M = 10000
for (i in 1:M) {x <- runif(1, -1,1); y <- runif(1, -1,1); d <- x*x+y*y
if(d < 1){n <- n+1; Dot(x,y,"brown"); if(d < 0.25) ok <- ok+1}}
cat("n.throws ",n," %OK ",ok/n*100,"\n")
#
BF=3;HF=3; BOXW(-1,1, -1,1)
type(-1,1,"-1"); type(1,1,"1"); type(-1,-1,"-1"); type(1,-1,"1")
circle(0,0, 1, "brown"); circle(0,0, 1/2, "brown"); BOX()
ok = 0; n = 10000
for(i in 1:n) {r <- runif(1); a <- runif(1, 0,pi*2); x <- r*cos(a); y <- r*sin(a)
d <- x*x+y*y; Dot(x,y,"brown"); if(d < 0.25) ok <- ok+1}
cat("n.throws ",n," %OK ",ok/n*100,"\n")
 n.throws 7851 %OK 25.11782 (-> 1/4) n.throws 10000 %OK 49.7 (-> 1/2)
# The three-dimensional representation (how to get it):
n.throws 7851 %OK 25.11782 (-> 1/4) n.throws 10000 %OK 49.7 (-> 1/2)
# The three-dimensional representation (how to get it):
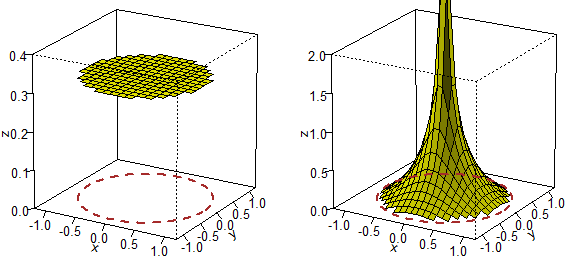 # ---------- ---------- ---------- ----------
# Here we saw how to use arrays. We go deep into the topic.
z = c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4)
t = array(z,dim=c(6,4)); t
[,1] [,2] [,3] [,4]
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
# To see the table in a different way:
data.entry(t)
# ---------- ---------- ---------- ----------
# Here we saw how to use arrays. We go deep into the topic.
z = c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4)
t = array(z,dim=c(6,4)); t
[,1] [,2] [,3] [,4]
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
# To see the table in a different way:
data.entry(t)
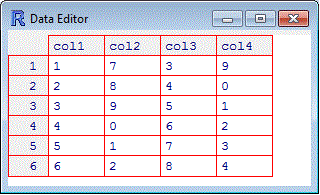 # We can also use data.entry to insert data:
t = array(dim=c(6,4)); data.entry(t)
# We can also use data.entry to insert data:
t = array(dim=c(6,4)); data.entry(t)
 # I insert data into the cells. Then I click [X] and:
t
var1 var2 var3 var4
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# An analysis of the columns
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# how to analyze the data in the first column
a = t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# and in the 6th row
b = t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# ---------- ---------- ---------- ----------
# See here for the histograms 3D (hist3d) and for the mosaic graphs (and for table).
[,1] [,2] males females
[1,] 603 246 primary 2.63 1.07 The distribution of 2nd col
[2,] 5051 1311 secondary 22.06 5.73 primary secondary tertiary
[3,] 7787 7901 tertiary 34.01 34.50 2.6 13.9 83.5
# I insert data into the cells. Then I click [X] and:
t
var1 var2 var3 var4
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# An analysis of the columns
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# how to analyze the data in the first column
a = t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# and in the 6th row
b = t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# ---------- ---------- ---------- ----------
# See here for the histograms 3D (hist3d) and for the mosaic graphs (and for table).
[,1] [,2] males females
[1,] 603 246 primary 2.63 1.07 The distribution of 2nd col
[2,] 5051 1311 secondary 22.06 5.73 primary secondary tertiary
[3,] 7787 7901 tertiary 34.01 34.50 2.6 13.9 83.5
 # ---------- ---------- ---------- ----------
# The program can analyze almost any stored data. We see an example where we use the
# readLines command to analyze the files and the read.table command to load them:
# [you can run help(read.table) for details; with n=… I avoid the possibility of
# filling the screen with many data; see here to use scan to load data not
# presented in a table]
readLines("http://macosa.dima.unige.it/R/pulse.txt",n=11)
[1] "# Survey of students in a university course, from the MiniTab manual"
[2] "# Heartbeats before an eventual 1 minute run"
[3] "# Heartbeats after"
[4] "# Did the student run? (1 yes; 0 no; according to the cast of a coin)"
[5] "# Is the student a smoker? (1 yes; 0 no)"
[6] "# the sex (1 M; 2 F)"
[7] "# height"
[8] "# weight"
[9] "# physical activity (0 nothing; 1 little; 2 middling; 3 a lot)"
[10] "Num,BeatBef,BeatAft,Run,Smoke,Sex,Heig,Weig,Phis"
[11] "01,64,88,1,0,1,168,64,2"
# In read.table I put header=FALSE to indicate that there is no column header that
# contains the names of the variables, skip=10 to indicate how many lines to skip
# before beginning to read data, sep="," to indicate the character that separes the
# data:
da= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=FALSE,skip=10,sep =",")
da
V1 V2 V3 V4 V5 V6 V7 V8 V9
1 1 64 88 1 0 1 168 64 2
2 2 58 70 1 0 1 183 66 2
3 3 62 76 1 1 1 186 73 3
4 4 66 78 1 1 1 184 86 1
5 5 64 80 1 0 1 176 70 2
6 6 74 84 1 0 1 184 75 1
7 7 84 84 1 0 1 184 68 3
...
89 89 78 80 0 0 2 173 60 1
90 90 68 68 0 0 2 159 50 2
91 91 86 84 0 0 2 171 68 3
92 92 76 76 0 0 2 156 49 2
# To understand what we are analyzing we use str:
str(da)
'data.frame': 92 obs. of 8 variables:
$ V1: int 1 2 3 4 5 6 7 8 9 10 ...
$ V2: int 64 58 62 66 64 74 84 68 62 76 ...
$ V3: int 88 70 76 78 80 84 84 72 75 118 ...
$ V4: int 1 1 1 1 1 1 1 1 1 1 ...
$ V5: int 0 0 1 1 0 0 0 0 0 0 ...
$ V6: int 1 1 1 1 1 1 1 1 1 1 ...
$ V7: int 168 183 186 184 176 184 184 188 184 181 ...
$ V8: int 64 66 73 86 70 75 68 86 88 63 ...
$ V9: int 2 2 3 1 2 1 3 2 2 2 ...
# The columns, without headers, are automatically headed (V1, … , V9)
summary(da[2:9])
V2 V3 V4 V5
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V6 V7 V8 V9
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# I can examine a single variable (the heartbeats at rest):
bb = da$V2; summary(bb)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(bb)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
#
# If I want, I can use headers (before the data). In this case they already are: Num, …
dat= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=TRUE,skip=9,sep =",")
str(dat)
'data.frame': 92 obs. of 9 variables:
$ Num : int 1 2 3 4 5 6 7 8 9 10 ...
$ BeatBef: int 64 58 62 66 64 74 84 68 62 76 ...
$ BeatAft: int 88 70 76 78 80 84 84 72 75 118 ...
$ Run : int 1 1 1 1 1 1 1 1 1 1 ...
$ Smoke : int 0 0 1 1 0 0 0 0 0 0 ...
$ Sex : int 1 1 1 1 1 1 1 1 1 1 ...
$ Heig : int 168 183 186 184 176 184 184 188 184 181 ...
$ Weig : int 64 66 73 86 70 75 68 86 88 63 ...
$ Phis : int 2 2 3 1 2 1 3 2 2 2 ...
summary(dat$BeatBef)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
#
# I can extract the data (of heartbeats at rest) of males or females:
hm = subset(bb,da$V6==1); hf = subset(bb,da$V6==2)
# Their histograms in the same scale:
dev.new(); hist(hm,right=FALSE,probability=TRUE,border="blue",col="cyan",
xlim=c(45,100),ylim=c(0,0.055)); BOX() # With BOX I add a grid
dev.new(); hist(hf,right=FALSE,probability=TRUE,border="brown",col="pink",
xlim=c(45,100),ylim=c(0,0.055)); BOX()
# ---------- ---------- ---------- ----------
# The program can analyze almost any stored data. We see an example where we use the
# readLines command to analyze the files and the read.table command to load them:
# [you can run help(read.table) for details; with n=… I avoid the possibility of
# filling the screen with many data; see here to use scan to load data not
# presented in a table]
readLines("http://macosa.dima.unige.it/R/pulse.txt",n=11)
[1] "# Survey of students in a university course, from the MiniTab manual"
[2] "# Heartbeats before an eventual 1 minute run"
[3] "# Heartbeats after"
[4] "# Did the student run? (1 yes; 0 no; according to the cast of a coin)"
[5] "# Is the student a smoker? (1 yes; 0 no)"
[6] "# the sex (1 M; 2 F)"
[7] "# height"
[8] "# weight"
[9] "# physical activity (0 nothing; 1 little; 2 middling; 3 a lot)"
[10] "Num,BeatBef,BeatAft,Run,Smoke,Sex,Heig,Weig,Phis"
[11] "01,64,88,1,0,1,168,64,2"
# In read.table I put header=FALSE to indicate that there is no column header that
# contains the names of the variables, skip=10 to indicate how many lines to skip
# before beginning to read data, sep="," to indicate the character that separes the
# data:
da= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=FALSE,skip=10,sep =",")
da
V1 V2 V3 V4 V5 V6 V7 V8 V9
1 1 64 88 1 0 1 168 64 2
2 2 58 70 1 0 1 183 66 2
3 3 62 76 1 1 1 186 73 3
4 4 66 78 1 1 1 184 86 1
5 5 64 80 1 0 1 176 70 2
6 6 74 84 1 0 1 184 75 1
7 7 84 84 1 0 1 184 68 3
...
89 89 78 80 0 0 2 173 60 1
90 90 68 68 0 0 2 159 50 2
91 91 86 84 0 0 2 171 68 3
92 92 76 76 0 0 2 156 49 2
# To understand what we are analyzing we use str:
str(da)
'data.frame': 92 obs. of 8 variables:
$ V1: int 1 2 3 4 5 6 7 8 9 10 ...
$ V2: int 64 58 62 66 64 74 84 68 62 76 ...
$ V3: int 88 70 76 78 80 84 84 72 75 118 ...
$ V4: int 1 1 1 1 1 1 1 1 1 1 ...
$ V5: int 0 0 1 1 0 0 0 0 0 0 ...
$ V6: int 1 1 1 1 1 1 1 1 1 1 ...
$ V7: int 168 183 186 184 176 184 184 188 184 181 ...
$ V8: int 64 66 73 86 70 75 68 86 88 63 ...
$ V9: int 2 2 3 1 2 1 3 2 2 2 ...
# The columns, without headers, are automatically headed (V1, … , V9)
summary(da[2:9])
V2 V3 V4 V5
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V6 V7 V8 V9
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# I can examine a single variable (the heartbeats at rest):
bb = da$V2; summary(bb)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(bb)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
#
# If I want, I can use headers (before the data). In this case they already are: Num, …
dat= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=TRUE,skip=9,sep =",")
str(dat)
'data.frame': 92 obs. of 9 variables:
$ Num : int 1 2 3 4 5 6 7 8 9 10 ...
$ BeatBef: int 64 58 62 66 64 74 84 68 62 76 ...
$ BeatAft: int 88 70 76 78 80 84 84 72 75 118 ...
$ Run : int 1 1 1 1 1 1 1 1 1 1 ...
$ Smoke : int 0 0 1 1 0 0 0 0 0 0 ...
$ Sex : int 1 1 1 1 1 1 1 1 1 1 ...
$ Heig : int 168 183 186 184 176 184 184 188 184 181 ...
$ Weig : int 64 66 73 86 70 75 68 86 88 63 ...
$ Phis : int 2 2 3 1 2 1 3 2 2 2 ...
summary(dat$BeatBef)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
#
# I can extract the data (of heartbeats at rest) of males or females:
hm = subset(bb,da$V6==1); hf = subset(bb,da$V6==2)
# Their histograms in the same scale:
dev.new(); hist(hm,right=FALSE,probability=TRUE,border="blue",col="cyan",
xlim=c(45,100),ylim=c(0,0.055)); BOX() # With BOX I add a grid
dev.new(); hist(hf,right=FALSE,probability=TRUE,border="brown",col="pink",
xlim=c(45,100),ylim=c(0,0.055)); BOX()
 #
# How to determine the coefficient of correlation rX,Y between two variables X and Y?
#
# How to determine the coefficient of correlation rX,Y between two variables X and Y?
 # Some examples (rounding to 1st digit after "."):
# Some examples (rounding to 1st digit after "."):
 # We can explicitly define:
COR = function(X,Y) mean((X-mean(X))*(Y-mean(Y)))/(Sd(X)*Sd(Y))
[ see here ]
# Example of use:
h = da$V7; w = da$V8; COR(h,w) # correlation between heigth and weight
[1] 0.7826331
s = da$V5; p = da$V9; COR(s,p) # correlation between smoking and physical activity
[1] -0.1202018
# Or we can use the function cor. For example we can type cor(da) or:
print( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V3 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V4 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V5 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V6 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.709 -0.71023 -0.10497
V7 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V8 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V9 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
# or:
round( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V3 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V4 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V5 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V6 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V7 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V8 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V9 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
#
# The statistical correlation is not a substantial correlation!
# For example, let's examine separately the statistical correlation between weight and
# height for males and females:
M = subset(da,da$V6==1); F = subset(da,da$V6==2)
cor(M[7],M[8]); cor(F[7],F[8])
V8 V8
V7 0.5904648 V7 0.5191614
# They are both much less than 0.783!
# We can better understand the phenomenon with a graphic representation:
Plane(min(da[7]),max(da[7]),min(da[8]),max(da[8])); abovex("height"); abovey("weight")
POINT(F[,7],F[,8],"red"); Point(M[,7],M[,8],"blue")
# We can explicitly define:
COR = function(X,Y) mean((X-mean(X))*(Y-mean(Y)))/(Sd(X)*Sd(Y))
[ see here ]
# Example of use:
h = da$V7; w = da$V8; COR(h,w) # correlation between heigth and weight
[1] 0.7826331
s = da$V5; p = da$V9; COR(s,p) # correlation between smoking and physical activity
[1] -0.1202018
# Or we can use the function cor. For example we can type cor(da) or:
print( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V3 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V4 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V5 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V6 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.709 -0.71023 -0.10497
V7 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V8 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V9 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
# or:
round( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V3 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V4 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V5 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V6 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V7 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V8 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V9 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
#
# The statistical correlation is not a substantial correlation!
# For example, let's examine separately the statistical correlation between weight and
# height for males and females:
M = subset(da,da$V6==1); F = subset(da,da$V6==2)
cor(M[7],M[8]); cor(F[7],F[8])
V8 V8
V7 0.5904648 V7 0.5191614
# They are both much less than 0.783!
# We can better understand the phenomenon with a graphic representation:
Plane(min(da[7]),max(da[7]),min(da[8]),max(da[8])); abovex("height"); abovey("weight")
POINT(F[,7],F[,8],"red"); Point(M[,7],M[,8],"blue")
 # The problem is due to the presence of two subpopulations with different
# characteristics.
# How to associate a precision with cor? See down.
# ---------- ---------- ---------- ----------
# To study the relationship between a dependent variable y and an independent variable
# x we can use linear regression, ie (if (x1,y2),…,(xN,yN) are the experimental points)
# we can find the function F: x->ax+b such that (F(x1)-y1)²+…+(F(xN)-yN)² is minimum
# For instance we examine the same data (see).
H = da[,7]; W = da[,8]
Plane(min(H),max(H),min(W),max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown")
LR(H,W) # You obtain A and B, if y=A+Bx is the line
[1] -90.8681981 0.8983596
f = function(x) LR(H,W)[1]+LR(H,W)[2]*x; graph1(f,150,200,"blue")
# or: abline(LR(H,W), col="blue")
# The line passes through the centroid (see the picture in the center)
POINT(mean(H),mean(W),"blue")
# The problem is due to the presence of two subpopulations with different
# characteristics.
# How to associate a precision with cor? See down.
# ---------- ---------- ---------- ----------
# To study the relationship between a dependent variable y and an independent variable
# x we can use linear regression, ie (if (x1,y2),…,(xN,yN) are the experimental points)
# we can find the function F: x->ax+b such that (F(x1)-y1)²+…+(F(xN)-yN)² is minimum
# For instance we examine the same data (see).
H = da[,7]; W = da[,8]
Plane(min(H),max(H),min(W),max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown")
LR(H,W) # You obtain A and B, if y=A+Bx is the line
[1] -90.8681981 0.8983596
f = function(x) LR(H,W)[1]+LR(H,W)[2]*x; graph1(f,150,200,"blue")
# or: abline(LR(H,W), col="blue")
# The line passes through the centroid (see the picture in the center)
POINT(mean(H),mean(W),"blue")
 # We can consider the linear regression constrained to pass through (0,0) or through
# another point: it is the same problem with some constrains to F. The picture on the
# right illustrates two cases.
# Also for this linear regression the line passes through the centroid.
Plane(0,max(H),0,max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown"); graph1(f,0,200,"blue"); POINT(mean(H),mean(W),"blue")
POINT(0,0,"black"); LR0(H,W,0,0) # You obtain A and B, if y=A+Bx is the line
0 0.3789037 <- LR01 LR02 y=LR01+LR02*x
# [ We note that I can obtain 0.3789037 also by: mean(H*W)/mean(H^2) ]
A=LR01; B=LR02; g = function(x) A + B*x; graph1(g,0,200,"seagreen")
POINT(50,40,"black"); LR0(H,W,50,40)
29.42683 0.2114634 <- LR01 LR02 y=LR01+LR02*x
h = function(x) LR01+LR02*x; graph1(h,0,200,"red")
# How to associate a precision with LR and LR0? See down.
# We can compute linear regression with regression and regression1 too (see).
# ---------- ---------- ---------- ----------
# A more significant example.
readLines("http://macosa.dima.unige.it/R/callup.txt",n=11)
[1] "# Medical examination for call-up (Italian Navy - 1987 - first contingent)"
[2] "# (some chest measurements are unreliable; pay attention to that)"
[3] "# chest (truncated to cm)"
[4] "# weight (truncated to kg)"
[5] "# region (numbered on the basis of latitude of the chief town: 0ao 1tr 2fr"
[6] "# 3lomb 4ven 5piem 6em-rom 7lig 8tosc 9mar 10um 11abr 12laz 13pugl"
[7] "# 14camp 15sard 16cal 17sic; the other regions are not present)"
[8] "# height (truncated to cm and decreased by 100: 178 cm -> 78)"
[9] "chest; weight; region; height"
[10] "91;62;15;73"
[11] "86;64;15;70"
da <- read.table("http://macosa.dima.unige.it/R/callup.txt",skip=8, sep=";",header=TRUE)
str(da)
'data.frame': 4170 obs. of 4 variables:
$ chest : int 91 86 89 88 92 95 91 83 87 88 ...
$ weight: int 62 64 64 68 70 77 65 62 55 60 ...
$ region: int 15 15 15 15 15 15 15 15 15 15 ...
$ height: int 73 70 74 79 66 69 66 79 75 65 ...
# If I want to visualize the data in a different way:
# data.entry(da)
# We can consider the linear regression constrained to pass through (0,0) or through
# another point: it is the same problem with some constrains to F. The picture on the
# right illustrates two cases.
# Also for this linear regression the line passes through the centroid.
Plane(0,max(H),0,max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown"); graph1(f,0,200,"blue"); POINT(mean(H),mean(W),"blue")
POINT(0,0,"black"); LR0(H,W,0,0) # You obtain A and B, if y=A+Bx is the line
0 0.3789037 <- LR01 LR02 y=LR01+LR02*x
# [ We note that I can obtain 0.3789037 also by: mean(H*W)/mean(H^2) ]
A=LR01; B=LR02; g = function(x) A + B*x; graph1(g,0,200,"seagreen")
POINT(50,40,"black"); LR0(H,W,50,40)
29.42683 0.2114634 <- LR01 LR02 y=LR01+LR02*x
h = function(x) LR01+LR02*x; graph1(h,0,200,"red")
# How to associate a precision with LR and LR0? See down.
# We can compute linear regression with regression and regression1 too (see).
# ---------- ---------- ---------- ----------
# A more significant example.
readLines("http://macosa.dima.unige.it/R/callup.txt",n=11)
[1] "# Medical examination for call-up (Italian Navy - 1987 - first contingent)"
[2] "# (some chest measurements are unreliable; pay attention to that)"
[3] "# chest (truncated to cm)"
[4] "# weight (truncated to kg)"
[5] "# region (numbered on the basis of latitude of the chief town: 0ao 1tr 2fr"
[6] "# 3lomb 4ven 5piem 6em-rom 7lig 8tosc 9mar 10um 11abr 12laz 13pugl"
[7] "# 14camp 15sard 16cal 17sic; the other regions are not present)"
[8] "# height (truncated to cm and decreased by 100: 178 cm -> 78)"
[9] "chest; weight; region; height"
[10] "91;62;15;73"
[11] "86;64;15;70"
da <- read.table("http://macosa.dima.unige.it/R/callup.txt",skip=8, sep=";",header=TRUE)
str(da)
'data.frame': 4170 obs. of 4 variables:
$ chest : int 91 86 89 88 92 95 91 83 87 88 ...
$ weight: int 62 64 64 68 70 77 65 62 55 60 ...
$ region: int 15 15 15 15 15 15 15 15 15 15 ...
$ height: int 73 70 74 79 66 69 66 79 75 65 ...
# If I want to visualize the data in a different way:
# data.entry(da)
 summary(da)
chest weight region height
Min. : 48.00 Min. : 48.00 Min. : 0.00 Min. :47.00
1st Qu.: 86.00 1st Qu.: 63.00 1st Qu.: 7.00 1st Qu.:70.00
Median : 90.00 Median : 70.00 Median :12.00 Median :74.00
Mean : 91.19 Mean : 70.48 Mean :10.18 Mean :74.42
3rd Qu.: 95.00 3rd Qu.: 76.00 3rd Qu.:14.00 3rd Qu.:79.00
Max. :179.00 Max. :126.00 Max. :17.00 Max. :96.00
# We add 1/2 to truncated data, so we do not have to add 1/2 to the average values
# we get
da$chest <- da$chest+1/2; da$weight <- da$weight+1/2; da$height <- da$height+1/2
summary(da)
chest weight region height
Min. : 48.50 Min. : 48.50 Min. : 0.00 Min. :47.50
1st Qu.: 86.50 1st Qu.: 63.50 1st Qu.: 7.00 1st Qu.:70.50
Median : 90.50 Median : 70.50 Median :12.00 Median :74.50
Mean : 91.69 Mean : 70.98 Mean :10.18 Mean :74.92
3rd Qu.: 95.50 3rd Qu.: 76.50 3rd Qu.:14.00 3rd Qu.:79.50
Max. :179.50 Max. :126.50 Max. :17.00 Max. :96.50
round( cor(da), 3)
chest weight region height
chest 1.000 0.697 0.016 0.255
weight 0.697 1.000 0.023 0.458
region 0.016 0.023 1.000 -0.152
height 0.255 0.458 -0.152 1.000
#
# Let's shorten the names, to study the regression:
C = da$chest; W = da$weight; R = da$region; H = da$height
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5); Point(C,W,"magenta")
LR(C,W)
[1] -15.300034 0.940987
f = function(x) LR(C,W)[1]+LR(C,W)[2]*x; graph1(f,50,200,"black")
# Let's study the inverse relationship, too:
LR(W,C)
[1] 54.9919381 0.5170087
g = function(y) LR(W,C)[1]+LR(W,C)[2]*y
# We must represent the inverse relation (x <-> y).
# We represent it as CURVE instead of function
G = function(x,y) x - g(y); CUR(G,"seagreen")
POINT(mean(C),mean(W),"blue")
summary(da)
chest weight region height
Min. : 48.00 Min. : 48.00 Min. : 0.00 Min. :47.00
1st Qu.: 86.00 1st Qu.: 63.00 1st Qu.: 7.00 1st Qu.:70.00
Median : 90.00 Median : 70.00 Median :12.00 Median :74.00
Mean : 91.19 Mean : 70.48 Mean :10.18 Mean :74.42
3rd Qu.: 95.00 3rd Qu.: 76.00 3rd Qu.:14.00 3rd Qu.:79.00
Max. :179.00 Max. :126.00 Max. :17.00 Max. :96.00
# We add 1/2 to truncated data, so we do not have to add 1/2 to the average values
# we get
da$chest <- da$chest+1/2; da$weight <- da$weight+1/2; da$height <- da$height+1/2
summary(da)
chest weight region height
Min. : 48.50 Min. : 48.50 Min. : 0.00 Min. :47.50
1st Qu.: 86.50 1st Qu.: 63.50 1st Qu.: 7.00 1st Qu.:70.50
Median : 90.50 Median : 70.50 Median :12.00 Median :74.50
Mean : 91.69 Mean : 70.98 Mean :10.18 Mean :74.92
3rd Qu.: 95.50 3rd Qu.: 76.50 3rd Qu.:14.00 3rd Qu.:79.50
Max. :179.50 Max. :126.50 Max. :17.00 Max. :96.50
round( cor(da), 3)
chest weight region height
chest 1.000 0.697 0.016 0.255
weight 0.697 1.000 0.023 0.458
region 0.016 0.023 1.000 -0.152
height 0.255 0.458 -0.152 1.000
#
# Let's shorten the names, to study the regression:
C = da$chest; W = da$weight; R = da$region; H = da$height
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5); Point(C,W,"magenta")
LR(C,W)
[1] -15.300034 0.940987
f = function(x) LR(C,W)[1]+LR(C,W)[2]*x; graph1(f,50,200,"black")
# Let's study the inverse relationship, too:
LR(W,C)
[1] 54.9919381 0.5170087
g = function(y) LR(W,C)[1]+LR(W,C)[2]*y
# We must represent the inverse relation (x <-> y).
# We represent it as CURVE instead of function
G = function(x,y) x - g(y); CUR(G,"seagreen")
POINT(mean(C),mean(W),"blue")
 # If we have a large numbers of points we can use more or less dense colors according
# to the frequency. We have two chances. The first (picture in the middle):
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, Dcol(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown"); POINT(mean(C),mean(W),"red")
# The second (picture on the right)
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, DCOL(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown")
#
# Let's see the histograms of height and weight, too:
dev.new(); hist(H,right=FALSE,probability=TRUE,col="grey");BOX()
dev.new(); hist(W,right=FALSE,probability=TRUE,col="grey");BOX()
# If we have a large numbers of points we can use more or less dense colors according
# to the frequency. We have two chances. The first (picture in the middle):
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, Dcol(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown"); POINT(mean(C),mean(W),"red")
# The second (picture on the right)
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, DCOL(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown")
#
# Let's see the histograms of height and weight, too:
dev.new(); hist(H,right=FALSE,probability=TRUE,col="grey");BOX()
dev.new(); hist(W,right=FALSE,probability=TRUE,col="grey");BOX()
 # The histogram of chest is hampered by not reliable data.
# Well, I cut off the tails:
dev.new(); hist(C,right=FALSE,probability=TRUE,col="grey");BOX()
C2=0; for(i in 1:4140) C2[i]=C1[i+15]
dev.new(); hist(C2,nclass=15,right=FALSE,probability=TRUE,col="grey");BOX()
# The histogram of chest is hampered by not reliable data.
# Well, I cut off the tails:
dev.new(); hist(C,right=FALSE,probability=TRUE,col="grey");BOX()
C2=0; for(i in 1:4140) C2[i]=C1[i+15]
dev.new(); hist(C2,nclass=15,right=FALSE,probability=TRUE,col="grey");BOX()
 # ---------- ---------- ---------- ----------
# QQ plot (quantiles against quantiles plot) is an instrument sometimes employed to
# compare distributions.
# An example of use (referring to the previuos data).
HP=0; for(i in 1:19) HP[i] = Percentile(H,i*5)
WP=0; for(i in 1:19) WP[i] = Percentile(W,i*5)
CP=0; for(i in 1:19) CP[i] = Percentile(C,i*5)
# Some percentiles of the variables and their graphic comparison:
PlaneP(HP,WP); Point(HP,WP,"brown"); abovex("H");abovey("W")
PlaneP(HP,CP); Point(HP,CP,"brown"); abovex("H");abovey("C")
PlaneP(WP,CP); Point(WP,CP,"brown"); abovex("W");abovey("C")
# ---------- ---------- ---------- ----------
# QQ plot (quantiles against quantiles plot) is an instrument sometimes employed to
# compare distributions.
# An example of use (referring to the previuos data).
HP=0; for(i in 1:19) HP[i] = Percentile(H,i*5)
WP=0; for(i in 1:19) WP[i] = Percentile(W,i*5)
CP=0; for(i in 1:19) CP[i] = Percentile(C,i*5)
# Some percentiles of the variables and their graphic comparison:
PlaneP(HP,WP); Point(HP,WP,"brown"); abovex("H");abovey("W")
PlaneP(HP,CP); Point(HP,CP,"brown"); abovex("H");abovey("C")
PlaneP(WP,CP); Point(WP,CP,"brown"); abovex("W");abovey("C")
 # As we have seen (better) comparing the histograms, I find that W and C have a
# similar distribution.
# ---------- ---------- ---------- ----------
# Still something about the study of the relation between two variables.
# As we have seen (better) comparing the histograms, I find that W and C have a
# similar distribution.
# ---------- ---------- ---------- ----------
# Still something about the study of the relation between two variables.
# I hang different
# objects to an elastic.
# Let F be the weight (in
# g) of the objects, let
# H be the elongation
# (in mm) of the elastic.
|
H | F
15 | 260
20 | 380
39 | 710
52 | 990 |  |
 |
# If I know that the values of H are ±2 and the values of F are ±5 I can proceed as we
# saw here:
H = c(15,20,39,52); F = c(260,380,710,990); eH = rep(2,4); eF = rep(5,4)
Plane(0,60, 0,1000); pointDif(0,0, H,F, eH,eF)
# 18.24074 * x
# 19.32432 * x
 # F = k·H, 18.240 ≤ k ≤ 19.325, or k = 18.8±0.6
#
# If I don't know the precision of the measurements I can proceed as we saw just above:
Plane(0,60, 0,1000); POINT(H,F, "brown"); abovex("H"); abovey("F")
LR(H,F) # if I don't know that for H=0 F=0
# -21.40182 19.25085
f = function(x) LR(H,F)[1]+LR(H,F)[2]*x; graph1(f,0,60,"red")
LR0(H,F, 0,0) # if I know that for H=0 F=0
# 0 18.69485 <- LR01 LR02 y=LR01+LR02*x
g = function(x) LR02*x; graph1(g,0,60,"seagreen")
# F = k·H, 18.240 ≤ k ≤ 19.325, or k = 18.8±0.6
#
# If I don't know the precision of the measurements I can proceed as we saw just above:
Plane(0,60, 0,1000); POINT(H,F, "brown"); abovex("H"); abovey("F")
LR(H,F) # if I don't know that for H=0 F=0
# -21.40182 19.25085
f = function(x) LR(H,F)[1]+LR(H,F)[2]*x; graph1(f,0,60,"red")
LR0(H,F, 0,0) # if I know that for H=0 F=0
# 0 18.69485 <- LR01 LR02 y=LR01+LR02*x
g = function(x) LR02*x; graph1(g,0,60,"seagreen")
 # To evaluate the goodness of approximation obtained with the regression line, I
# proceed as follows, in the first case (LR): (F function of H; first F, then H)
confInt(F,H, 90/100)
# 5 % 95 %
# (Intercept) -90.15108 47.34745
# Conf 17.27649 21.22522
# In the second case (LR0):
confInt0(F,H, 0,0, 90/100)
# 5 % 95 %
# Conf 18.03658 19.35311 (quite similar to 18.240 19.325)
# These are the confidence intervals at the 90% (0.9) significance level of the slope
# and (in the first case) of the intercept of the line. I can change the level.
# To evaluate the goodness of approximation obtained with the regression line, I
# proceed as follows, in the first case (LR): (F function of H; first F, then H)
confInt(F,H, 90/100)
# 5 % 95 %
# (Intercept) -90.15108 47.34745
# Conf 17.27649 21.22522
# In the second case (LR0):
confInt0(F,H, 0,0, 90/100)
# 5 % 95 %
# Conf 18.03658 19.35311 (quite similar to 18.240 19.325)
# These are the confidence intervals at the 90% (0.9) significance level of the slope
# and (in the first case) of the intercept of the line. I can change the level.
 # H and F are strongly correlated (see above):
cor(H,F)
# 0.9987686 (about 1)
# To value the efficacy of the correlation we determine a confidence interval
cor.test(H,F, conf.level=0.90)
# 90 percent confidence interval:
# 0.9674734 0.9999541 (comments on the other outputs)
# Another correlation coefficient often used is "Sperman's". It is indicated with ρ (the
# Greek letter "ro", which corresponds to our R) in that it compares the "ranks" of the
# data, ie not their values but their order number (1st, 2nd, ...). See here. An example:
x = c(10,20,30,40); y = c(15,60,70,200)
cor(x,y); cor(x,y, method="spearman")
# 0.9173057 1
# The data is arranged in an increasing way, but not aligned. The usual correlation
# coefficient is close to 1. The Spearman coefficient is instead just 1, indicating that
# the data is increasing, beyond the way they grow. Another example:
x = c(10,20,30,40,50); y = c(1,2,-900,3,4)
cor(x,y); cor(x,y, method="spearman")
# 0.002742232 0.7
# ---------- ---------- ---------- ----------
# For linear, quadratic and cubic regression and for spline see here
# ---------- ---------- ---------- ----------
# The coefficient of correlation can be found also for other type of function. An example.
# We can define:
COR2 = function(X,Y,f) {Sr=sum((y-f(x))^2);Sm=sum((Y-mean(Y))^2);sqrt((Sm-Sr)/Sm)}
# Or we can use the already defined function cor2
# We want compare the following data with the quadratic regression
x <- c(0,1,2,3,4,5); y <- c(2.1,7.7,13.6,27.2,40.9,61.1)
Plane(-1,6, 0,70); POINT(x,y, "blue")
regression2(x,y)
# 1.86 * x^2 + 2.36 * x + 2.48
f=function(x) 1.86 * x^2 + 2.36 * x + 2.48; graph1(f,-1,6, "black")
cor2(x,y,f)
# 0.9992544 A value near to 1! With linear regression I have:
cor(x,y)
# 0.9731813
# I can obtain the same value with cor2 if I put this function:
regression1(x,y)
# 11.66 * x + -3.724
g = function(x) 11.66 * x + -3.724; graph1(g,-1,6, "red")
cor2(x,y,g)
# 0.9731812
# H and F are strongly correlated (see above):
cor(H,F)
# 0.9987686 (about 1)
# To value the efficacy of the correlation we determine a confidence interval
cor.test(H,F, conf.level=0.90)
# 90 percent confidence interval:
# 0.9674734 0.9999541 (comments on the other outputs)
# Another correlation coefficient often used is "Sperman's". It is indicated with ρ (the
# Greek letter "ro", which corresponds to our R) in that it compares the "ranks" of the
# data, ie not their values but their order number (1st, 2nd, ...). See here. An example:
x = c(10,20,30,40); y = c(15,60,70,200)
cor(x,y); cor(x,y, method="spearman")
# 0.9173057 1
# The data is arranged in an increasing way, but not aligned. The usual correlation
# coefficient is close to 1. The Spearman coefficient is instead just 1, indicating that
# the data is increasing, beyond the way they grow. Another example:
x = c(10,20,30,40,50); y = c(1,2,-900,3,4)
cor(x,y); cor(x,y, method="spearman")
# 0.002742232 0.7
# ---------- ---------- ---------- ----------
# For linear, quadratic and cubic regression and for spline see here
# ---------- ---------- ---------- ----------
# The coefficient of correlation can be found also for other type of function. An example.
# We can define:
COR2 = function(X,Y,f) {Sr=sum((y-f(x))^2);Sm=sum((Y-mean(Y))^2);sqrt((Sm-Sr)/Sm)}
# Or we can use the already defined function cor2
# We want compare the following data with the quadratic regression
x <- c(0,1,2,3,4,5); y <- c(2.1,7.7,13.6,27.2,40.9,61.1)
Plane(-1,6, 0,70); POINT(x,y, "blue")
regression2(x,y)
# 1.86 * x^2 + 2.36 * x + 2.48
f=function(x) 1.86 * x^2 + 2.36 * x + 2.48; graph1(f,-1,6, "black")
cor2(x,y,f)
# 0.9992544 A value near to 1! With linear regression I have:
cor(x,y)
# 0.9731813
# I can obtain the same value with cor2 if I put this function:
regression1(x,y)
# 11.66 * x + -3.724
g = function(x) 11.66 * x + -3.724; graph1(g,-1,6, "red")
cor2(x,y,g)
# 0.9731812

 # But math is not enough! In the case of the picture on the right:
x <- c(0,1,2,3,4,5); y <- c(2,19,38,15,48,43)
Plane(-1,6, 0,50); POINT(x,y,"black")
regression1(x,y) # 7.686 * x + 8.286
f1=function(x) 7.686 * x + 8.286; graph1(f1,-1,6, "blue")
regression2(x,y) # -0.964 * x^2 + 12.5 * x + 5.07
f2=function(x) -0.964 * x^2 + 12.5 * x + 5.07; graph1(f2,-1,6, "brown")
regression3(x,y) # 0.87 * x^3 + -7.49 * x^2 + 24.4 * x + 2.46
f3=function(x) 0.87*x^3-7.49*x^2+24.4*x+2.46; graph1(f3,-1,6, "red")
cor2(x,y,f1); cor2(x,y,f2); cor2(x,y,f3)
# 0.7916388 0.8048205 0.8230846
# The cubic function gives a better correlation. But the type of function (a polynomial
# or other function) with which I can approximate the data depends on the context.
# But math is not enough! In the case of the picture on the right:
x <- c(0,1,2,3,4,5); y <- c(2,19,38,15,48,43)
Plane(-1,6, 0,50); POINT(x,y,"black")
regression1(x,y) # 7.686 * x + 8.286
f1=function(x) 7.686 * x + 8.286; graph1(f1,-1,6, "blue")
regression2(x,y) # -0.964 * x^2 + 12.5 * x + 5.07
f2=function(x) -0.964 * x^2 + 12.5 * x + 5.07; graph1(f2,-1,6, "brown")
regression3(x,y) # 0.87 * x^3 + -7.49 * x^2 + 24.4 * x + 2.46
f3=function(x) 0.87*x^3-7.49*x^2+24.4*x+2.46; graph1(f3,-1,6, "red")
cor2(x,y,f1); cor2(x,y,f2); cor2(x,y,f3)
# 0.7916388 0.8048205 0.8230846
# The cubic function gives a better correlation. But the type of function (a polynomial
# or other function) with which I can approximate the data depends on the context.
# For example, if I look for a function of the type
# x -> sin(U*x)+V*x I find x -> sin(3.58*x)+9.98*x
# (see here). I obtain a different correlation:
f=function(x) sin(3.58*x)+9.98*x; cor2(x,y,f)
# 0.768965
# If I look for a function of the type x -> U*x I find:
k=function(x) 9.94545*x; cor2(x,y, k)
# 0.7397531
 |
 |
# ---------- ---------- ---------- ----------
# Binomial and Gaussian distributions, Continuous case, Central limit theorem
# Exponential and Poisson distributions
# Test
Other examples of use
 n.throws 7851 %OK 25.11782 (-> 1/4) n.throws 10000 %OK 49.7 (-> 1/2)
# The three-dimensional representation (how to get it):
n.throws 7851 %OK 25.11782 (-> 1/4) n.throws 10000 %OK 49.7 (-> 1/2)
# The three-dimensional representation (how to get it):
 # ---------- ---------- ---------- ----------
# Here we saw how to use arrays. We go deep into the topic.
z = c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4)
t = array(z,dim=c(6,4)); t
[,1] [,2] [,3] [,4]
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
# To see the table in a different way:
data.entry(t)
# ---------- ---------- ---------- ----------
# Here we saw how to use arrays. We go deep into the topic.
z = c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4)
t = array(z,dim=c(6,4)); t
[,1] [,2] [,3] [,4]
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
# To see the table in a different way:
data.entry(t)
 # We can also use data.entry to insert data:
t = array(dim=c(6,4)); data.entry(t)
# We can also use data.entry to insert data:
t = array(dim=c(6,4)); data.entry(t)
 # I insert data into the cells. Then I click [X] and:
t
var1 var2 var3 var4
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# An analysis of the columns
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# how to analyze the data in the first column
a = t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# and in the 6th row
b = t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# ---------- ---------- ---------- ----------
# See here for the histograms 3D (hist3d) and for the mosaic graphs (and for table).
[,1] [,2] males females
[1,] 603 246 primary 2.63 1.07 The distribution of 2nd col
[2,] 5051 1311 secondary 22.06 5.73 primary secondary tertiary
[3,] 7787 7901 tertiary 34.01 34.50 2.6 13.9 83.5
# I insert data into the cells. Then I click [X] and:
t
var1 var2 var3 var4
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# An analysis of the columns
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# how to analyze the data in the first column
a = t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# and in the 6th row
b = t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# ---------- ---------- ---------- ----------
# See here for the histograms 3D (hist3d) and for the mosaic graphs (and for table).
[,1] [,2] males females
[1,] 603 246 primary 2.63 1.07 The distribution of 2nd col
[2,] 5051 1311 secondary 22.06 5.73 primary secondary tertiary
[3,] 7787 7901 tertiary 34.01 34.50 2.6 13.9 83.5
 # ---------- ---------- ---------- ----------
# The program can analyze almost any stored data. We see an example where we use the
# readLines command to analyze the files and the read.table command to load them:
# [you can run help(read.table) for details; with n=… I avoid the possibility of
# filling the screen with many data; see here to use scan to load data not
# presented in a table]
readLines("http://macosa.dima.unige.it/R/pulse.txt",n=11)
[1] "# Survey of students in a university course, from the MiniTab manual"
[2] "# Heartbeats before an eventual 1 minute run"
[3] "# Heartbeats after"
[4] "# Did the student run? (1 yes; 0 no; according to the cast of a coin)"
[5] "# Is the student a smoker? (1 yes; 0 no)"
[6] "# the sex (1 M; 2 F)"
[7] "# height"
[8] "# weight"
[9] "# physical activity (0 nothing; 1 little; 2 middling; 3 a lot)"
[10] "Num,BeatBef,BeatAft,Run,Smoke,Sex,Heig,Weig,Phis"
[11] "01,64,88,1,0,1,168,64,2"
# In read.table I put header=FALSE to indicate that there is no column header that
# contains the names of the variables, skip=10 to indicate how many lines to skip
# before beginning to read data, sep="," to indicate the character that separes the
# data:
da= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=FALSE,skip=10,sep =",")
da
V1 V2 V3 V4 V5 V6 V7 V8 V9
1 1 64 88 1 0 1 168 64 2
2 2 58 70 1 0 1 183 66 2
3 3 62 76 1 1 1 186 73 3
4 4 66 78 1 1 1 184 86 1
5 5 64 80 1 0 1 176 70 2
6 6 74 84 1 0 1 184 75 1
7 7 84 84 1 0 1 184 68 3
...
89 89 78 80 0 0 2 173 60 1
90 90 68 68 0 0 2 159 50 2
91 91 86 84 0 0 2 171 68 3
92 92 76 76 0 0 2 156 49 2
# To understand what we are analyzing we use str:
str(da)
'data.frame': 92 obs. of 8 variables:
$ V1: int 1 2 3 4 5 6 7 8 9 10 ...
$ V2: int 64 58 62 66 64 74 84 68 62 76 ...
$ V3: int 88 70 76 78 80 84 84 72 75 118 ...
$ V4: int 1 1 1 1 1 1 1 1 1 1 ...
$ V5: int 0 0 1 1 0 0 0 0 0 0 ...
$ V6: int 1 1 1 1 1 1 1 1 1 1 ...
$ V7: int 168 183 186 184 176 184 184 188 184 181 ...
$ V8: int 64 66 73 86 70 75 68 86 88 63 ...
$ V9: int 2 2 3 1 2 1 3 2 2 2 ...
# The columns, without headers, are automatically headed (V1, … , V9)
summary(da[2:9])
V2 V3 V4 V5
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V6 V7 V8 V9
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# I can examine a single variable (the heartbeats at rest):
bb = da$V2; summary(bb)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(bb)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
#
# If I want, I can use headers (before the data). In this case they already are: Num, …
dat= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=TRUE,skip=9,sep =",")
str(dat)
'data.frame': 92 obs. of 9 variables:
$ Num : int 1 2 3 4 5 6 7 8 9 10 ...
$ BeatBef: int 64 58 62 66 64 74 84 68 62 76 ...
$ BeatAft: int 88 70 76 78 80 84 84 72 75 118 ...
$ Run : int 1 1 1 1 1 1 1 1 1 1 ...
$ Smoke : int 0 0 1 1 0 0 0 0 0 0 ...
$ Sex : int 1 1 1 1 1 1 1 1 1 1 ...
$ Heig : int 168 183 186 184 176 184 184 188 184 181 ...
$ Weig : int 64 66 73 86 70 75 68 86 88 63 ...
$ Phis : int 2 2 3 1 2 1 3 2 2 2 ...
summary(dat$BeatBef)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
#
# I can extract the data (of heartbeats at rest) of males or females:
hm = subset(bb,da$V6==1); hf = subset(bb,da$V6==2)
# Their histograms in the same scale:
dev.new(); hist(hm,right=FALSE,probability=TRUE,border="blue",col="cyan",
xlim=c(45,100),ylim=c(0,0.055)); BOX() # With BOX I add a grid
dev.new(); hist(hf,right=FALSE,probability=TRUE,border="brown",col="pink",
xlim=c(45,100),ylim=c(0,0.055)); BOX()
# ---------- ---------- ---------- ----------
# The program can analyze almost any stored data. We see an example where we use the
# readLines command to analyze the files and the read.table command to load them:
# [you can run help(read.table) for details; with n=… I avoid the possibility of
# filling the screen with many data; see here to use scan to load data not
# presented in a table]
readLines("http://macosa.dima.unige.it/R/pulse.txt",n=11)
[1] "# Survey of students in a university course, from the MiniTab manual"
[2] "# Heartbeats before an eventual 1 minute run"
[3] "# Heartbeats after"
[4] "# Did the student run? (1 yes; 0 no; according to the cast of a coin)"
[5] "# Is the student a smoker? (1 yes; 0 no)"
[6] "# the sex (1 M; 2 F)"
[7] "# height"
[8] "# weight"
[9] "# physical activity (0 nothing; 1 little; 2 middling; 3 a lot)"
[10] "Num,BeatBef,BeatAft,Run,Smoke,Sex,Heig,Weig,Phis"
[11] "01,64,88,1,0,1,168,64,2"
# In read.table I put header=FALSE to indicate that there is no column header that
# contains the names of the variables, skip=10 to indicate how many lines to skip
# before beginning to read data, sep="," to indicate the character that separes the
# data:
da= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=FALSE,skip=10,sep =",")
da
V1 V2 V3 V4 V5 V6 V7 V8 V9
1 1 64 88 1 0 1 168 64 2
2 2 58 70 1 0 1 183 66 2
3 3 62 76 1 1 1 186 73 3
4 4 66 78 1 1 1 184 86 1
5 5 64 80 1 0 1 176 70 2
6 6 74 84 1 0 1 184 75 1
7 7 84 84 1 0 1 184 68 3
...
89 89 78 80 0 0 2 173 60 1
90 90 68 68 0 0 2 159 50 2
91 91 86 84 0 0 2 171 68 3
92 92 76 76 0 0 2 156 49 2
# To understand what we are analyzing we use str:
str(da)
'data.frame': 92 obs. of 8 variables:
$ V1: int 1 2 3 4 5 6 7 8 9 10 ...
$ V2: int 64 58 62 66 64 74 84 68 62 76 ...
$ V3: int 88 70 76 78 80 84 84 72 75 118 ...
$ V4: int 1 1 1 1 1 1 1 1 1 1 ...
$ V5: int 0 0 1 1 0 0 0 0 0 0 ...
$ V6: int 1 1 1 1 1 1 1 1 1 1 ...
$ V7: int 168 183 186 184 176 184 184 188 184 181 ...
$ V8: int 64 66 73 86 70 75 68 86 88 63 ...
$ V9: int 2 2 3 1 2 1 3 2 2 2 ...
# The columns, without headers, are automatically headed (V1, … , V9)
summary(da[2:9])
V2 V3 V4 V5
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V6 V7 V8 V9
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# I can examine a single variable (the heartbeats at rest):
bb = da$V2; summary(bb)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(bb)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
#
# If I want, I can use headers (before the data). In this case they already are: Num, …
dat= read.table("http://macosa.dima.unige.it/R/pulse.txt",header=TRUE,skip=9,sep =",")
str(dat)
'data.frame': 92 obs. of 9 variables:
$ Num : int 1 2 3 4 5 6 7 8 9 10 ...
$ BeatBef: int 64 58 62 66 64 74 84 68 62 76 ...
$ BeatAft: int 88 70 76 78 80 84 84 72 75 118 ...
$ Run : int 1 1 1 1 1 1 1 1 1 1 ...
$ Smoke : int 0 0 1 1 0 0 0 0 0 0 ...
$ Sex : int 1 1 1 1 1 1 1 1 1 1 ...
$ Heig : int 168 183 186 184 176 184 184 188 184 181 ...
$ Weig : int 64 66 73 86 70 75 68 86 88 63 ...
$ Phis : int 2 2 3 1 2 1 3 2 2 2 ...
summary(dat$BeatBef)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
#
# I can extract the data (of heartbeats at rest) of males or females:
hm = subset(bb,da$V6==1); hf = subset(bb,da$V6==2)
# Their histograms in the same scale:
dev.new(); hist(hm,right=FALSE,probability=TRUE,border="blue",col="cyan",
xlim=c(45,100),ylim=c(0,0.055)); BOX() # With BOX I add a grid
dev.new(); hist(hf,right=FALSE,probability=TRUE,border="brown",col="pink",
xlim=c(45,100),ylim=c(0,0.055)); BOX()
 #
# How to determine the coefficient of correlation rX,Y between two variables X and Y?
#
# How to determine the coefficient of correlation rX,Y between two variables X and Y?
 # Some examples (rounding to 1st digit after "."):
# Some examples (rounding to 1st digit after "."):
 # We can explicitly define:
COR = function(X,Y) mean((X-mean(X))*(Y-mean(Y)))/(Sd(X)*Sd(Y))
[ see here ]
# Example of use:
h = da$V7; w = da$V8; COR(h,w) # correlation between heigth and weight
[1] 0.7826331
s = da$V5; p = da$V9; COR(s,p) # correlation between smoking and physical activity
[1] -0.1202018
# Or we can use the function cor. For example we can type cor(da) or:
print( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V3 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V4 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V5 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V6 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.709 -0.71023 -0.10497
V7 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V8 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V9 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
# or:
round( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V3 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V4 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V5 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V6 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V7 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V8 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V9 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
#
# The statistical correlation is not a substantial correlation!
# For example, let's examine separately the statistical correlation between weight and
# height for males and females:
M = subset(da,da$V6==1); F = subset(da,da$V6==2)
cor(M[7],M[8]); cor(F[7],F[8])
V8 V8
V7 0.5904648 V7 0.5191614
# They are both much less than 0.783!
# We can better understand the phenomenon with a graphic representation:
Plane(min(da[7]),max(da[7]),min(da[8]),max(da[8])); abovex("height"); abovey("weight")
POINT(F[,7],F[,8],"red"); Point(M[,7],M[,8],"blue")
# We can explicitly define:
COR = function(X,Y) mean((X-mean(X))*(Y-mean(Y)))/(Sd(X)*Sd(Y))
[ see here ]
# Example of use:
h = da$V7; w = da$V8; COR(h,w) # correlation between heigth and weight
[1] 0.7826331
s = da$V5; p = da$V9; COR(s,p) # correlation between smoking and physical activity
[1] -0.1202018
# Or we can use the function cor. For example we can type cor(da) or:
print( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V3 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V4 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V5 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V6 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.709 -0.71023 -0.10497
V7 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V8 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V9 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
# or:
round( cor(da[2:9]), 3)
V2 V3 V4 V5 V6 V7 V8 V9
V2 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V3 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V4 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V5 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V6 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V7 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V8 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V9 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
#
# The statistical correlation is not a substantial correlation!
# For example, let's examine separately the statistical correlation between weight and
# height for males and females:
M = subset(da,da$V6==1); F = subset(da,da$V6==2)
cor(M[7],M[8]); cor(F[7],F[8])
V8 V8
V7 0.5904648 V7 0.5191614
# They are both much less than 0.783!
# We can better understand the phenomenon with a graphic representation:
Plane(min(da[7]),max(da[7]),min(da[8]),max(da[8])); abovex("height"); abovey("weight")
POINT(F[,7],F[,8],"red"); Point(M[,7],M[,8],"blue")
 # The problem is due to the presence of two subpopulations with different
# characteristics.
# How to associate a precision with cor? See down.
# ---------- ---------- ---------- ----------
# To study the relationship between a dependent variable y and an independent variable
# x we can use linear regression, ie (if (x1,y2),…,(xN,yN) are the experimental points)
# we can find the function F: x->ax+b such that (F(x1)-y1)²+…+(F(xN)-yN)² is minimum
# For instance we examine the same data (see).
H = da[,7]; W = da[,8]
Plane(min(H),max(H),min(W),max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown")
LR(H,W) # You obtain A and B, if y=A+Bx is the line
[1] -90.8681981 0.8983596
f = function(x) LR(H,W)[1]+LR(H,W)[2]*x; graph1(f,150,200,"blue")
# or: abline(LR(H,W), col="blue")
# The line passes through the centroid (see the picture in the center)
POINT(mean(H),mean(W),"blue")
# The problem is due to the presence of two subpopulations with different
# characteristics.
# How to associate a precision with cor? See down.
# ---------- ---------- ---------- ----------
# To study the relationship between a dependent variable y and an independent variable
# x we can use linear regression, ie (if (x1,y2),…,(xN,yN) are the experimental points)
# we can find the function F: x->ax+b such that (F(x1)-y1)²+…+(F(xN)-yN)² is minimum
# For instance we examine the same data (see).
H = da[,7]; W = da[,8]
Plane(min(H),max(H),min(W),max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown")
LR(H,W) # You obtain A and B, if y=A+Bx is the line
[1] -90.8681981 0.8983596
f = function(x) LR(H,W)[1]+LR(H,W)[2]*x; graph1(f,150,200,"blue")
# or: abline(LR(H,W), col="blue")
# The line passes through the centroid (see the picture in the center)
POINT(mean(H),mean(W),"blue")
 # We can consider the linear regression constrained to pass through (0,0) or through
# another point: it is the same problem with some constrains to F. The picture on the
# right illustrates two cases.
# Also for this linear regression the line passes through the centroid.
Plane(0,max(H),0,max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown"); graph1(f,0,200,"blue"); POINT(mean(H),mean(W),"blue")
POINT(0,0,"black"); LR0(H,W,0,0) # You obtain A and B, if y=A+Bx is the line
0 0.3789037 <- LR01 LR02 y=LR01+LR02*x
# [ We note that I can obtain 0.3789037 also by: mean(H*W)/mean(H^2) ]
A=LR01; B=LR02; g = function(x) A + B*x; graph1(g,0,200,"seagreen")
POINT(50,40,"black"); LR0(H,W,50,40)
29.42683 0.2114634 <- LR01 LR02 y=LR01+LR02*x
h = function(x) LR01+LR02*x; graph1(h,0,200,"red")
# How to associate a precision with LR and LR0? See down.
# We can compute linear regression with regression and regression1 too (see).
# ---------- ---------- ---------- ----------
# A more significant example.
readLines("http://macosa.dima.unige.it/R/callup.txt",n=11)
[1] "# Medical examination for call-up (Italian Navy - 1987 - first contingent)"
[2] "# (some chest measurements are unreliable; pay attention to that)"
[3] "# chest (truncated to cm)"
[4] "# weight (truncated to kg)"
[5] "# region (numbered on the basis of latitude of the chief town: 0ao 1tr 2fr"
[6] "# 3lomb 4ven 5piem 6em-rom 7lig 8tosc 9mar 10um 11abr 12laz 13pugl"
[7] "# 14camp 15sard 16cal 17sic; the other regions are not present)"
[8] "# height (truncated to cm and decreased by 100: 178 cm -> 78)"
[9] "chest; weight; region; height"
[10] "91;62;15;73"
[11] "86;64;15;70"
da <- read.table("http://macosa.dima.unige.it/R/callup.txt",skip=8, sep=";",header=TRUE)
str(da)
'data.frame': 4170 obs. of 4 variables:
$ chest : int 91 86 89 88 92 95 91 83 87 88 ...
$ weight: int 62 64 64 68 70 77 65 62 55 60 ...
$ region: int 15 15 15 15 15 15 15 15 15 15 ...
$ height: int 73 70 74 79 66 69 66 79 75 65 ...
# If I want to visualize the data in a different way:
# data.entry(da)
# We can consider the linear regression constrained to pass through (0,0) or through
# another point: it is the same problem with some constrains to F. The picture on the
# right illustrates two cases.
# Also for this linear regression the line passes through the centroid.
Plane(0,max(H),0,max(W)); abovex("height"); abovey("weight")
Point(H,W,"brown"); graph1(f,0,200,"blue"); POINT(mean(H),mean(W),"blue")
POINT(0,0,"black"); LR0(H,W,0,0) # You obtain A and B, if y=A+Bx is the line
0 0.3789037 <- LR01 LR02 y=LR01+LR02*x
# [ We note that I can obtain 0.3789037 also by: mean(H*W)/mean(H^2) ]
A=LR01; B=LR02; g = function(x) A + B*x; graph1(g,0,200,"seagreen")
POINT(50,40,"black"); LR0(H,W,50,40)
29.42683 0.2114634 <- LR01 LR02 y=LR01+LR02*x
h = function(x) LR01+LR02*x; graph1(h,0,200,"red")
# How to associate a precision with LR and LR0? See down.
# We can compute linear regression with regression and regression1 too (see).
# ---------- ---------- ---------- ----------
# A more significant example.
readLines("http://macosa.dima.unige.it/R/callup.txt",n=11)
[1] "# Medical examination for call-up (Italian Navy - 1987 - first contingent)"
[2] "# (some chest measurements are unreliable; pay attention to that)"
[3] "# chest (truncated to cm)"
[4] "# weight (truncated to kg)"
[5] "# region (numbered on the basis of latitude of the chief town: 0ao 1tr 2fr"
[6] "# 3lomb 4ven 5piem 6em-rom 7lig 8tosc 9mar 10um 11abr 12laz 13pugl"
[7] "# 14camp 15sard 16cal 17sic; the other regions are not present)"
[8] "# height (truncated to cm and decreased by 100: 178 cm -> 78)"
[9] "chest; weight; region; height"
[10] "91;62;15;73"
[11] "86;64;15;70"
da <- read.table("http://macosa.dima.unige.it/R/callup.txt",skip=8, sep=";",header=TRUE)
str(da)
'data.frame': 4170 obs. of 4 variables:
$ chest : int 91 86 89 88 92 95 91 83 87 88 ...
$ weight: int 62 64 64 68 70 77 65 62 55 60 ...
$ region: int 15 15 15 15 15 15 15 15 15 15 ...
$ height: int 73 70 74 79 66 69 66 79 75 65 ...
# If I want to visualize the data in a different way:
# data.entry(da)
 summary(da)
chest weight region height
Min. : 48.00 Min. : 48.00 Min. : 0.00 Min. :47.00
1st Qu.: 86.00 1st Qu.: 63.00 1st Qu.: 7.00 1st Qu.:70.00
Median : 90.00 Median : 70.00 Median :12.00 Median :74.00
Mean : 91.19 Mean : 70.48 Mean :10.18 Mean :74.42
3rd Qu.: 95.00 3rd Qu.: 76.00 3rd Qu.:14.00 3rd Qu.:79.00
Max. :179.00 Max. :126.00 Max. :17.00 Max. :96.00
# We add 1/2 to truncated data, so we do not have to add 1/2 to the average values
# we get
da$chest <- da$chest+1/2; da$weight <- da$weight+1/2; da$height <- da$height+1/2
summary(da)
chest weight region height
Min. : 48.50 Min. : 48.50 Min. : 0.00 Min. :47.50
1st Qu.: 86.50 1st Qu.: 63.50 1st Qu.: 7.00 1st Qu.:70.50
Median : 90.50 Median : 70.50 Median :12.00 Median :74.50
Mean : 91.69 Mean : 70.98 Mean :10.18 Mean :74.92
3rd Qu.: 95.50 3rd Qu.: 76.50 3rd Qu.:14.00 3rd Qu.:79.50
Max. :179.50 Max. :126.50 Max. :17.00 Max. :96.50
round( cor(da), 3)
chest weight region height
chest 1.000 0.697 0.016 0.255
weight 0.697 1.000 0.023 0.458
region 0.016 0.023 1.000 -0.152
height 0.255 0.458 -0.152 1.000
#
# Let's shorten the names, to study the regression:
C = da$chest; W = da$weight; R = da$region; H = da$height
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5); Point(C,W,"magenta")
LR(C,W)
[1] -15.300034 0.940987
f = function(x) LR(C,W)[1]+LR(C,W)[2]*x; graph1(f,50,200,"black")
# Let's study the inverse relationship, too:
LR(W,C)
[1] 54.9919381 0.5170087
g = function(y) LR(W,C)[1]+LR(W,C)[2]*y
# We must represent the inverse relation (x <-> y).
# We represent it as CURVE instead of function
G = function(x,y) x - g(y); CUR(G,"seagreen")
POINT(mean(C),mean(W),"blue")
summary(da)
chest weight region height
Min. : 48.00 Min. : 48.00 Min. : 0.00 Min. :47.00
1st Qu.: 86.00 1st Qu.: 63.00 1st Qu.: 7.00 1st Qu.:70.00
Median : 90.00 Median : 70.00 Median :12.00 Median :74.00
Mean : 91.19 Mean : 70.48 Mean :10.18 Mean :74.42
3rd Qu.: 95.00 3rd Qu.: 76.00 3rd Qu.:14.00 3rd Qu.:79.00
Max. :179.00 Max. :126.00 Max. :17.00 Max. :96.00
# We add 1/2 to truncated data, so we do not have to add 1/2 to the average values
# we get
da$chest <- da$chest+1/2; da$weight <- da$weight+1/2; da$height <- da$height+1/2
summary(da)
chest weight region height
Min. : 48.50 Min. : 48.50 Min. : 0.00 Min. :47.50
1st Qu.: 86.50 1st Qu.: 63.50 1st Qu.: 7.00 1st Qu.:70.50
Median : 90.50 Median : 70.50 Median :12.00 Median :74.50
Mean : 91.69 Mean : 70.98 Mean :10.18 Mean :74.92
3rd Qu.: 95.50 3rd Qu.: 76.50 3rd Qu.:14.00 3rd Qu.:79.50
Max. :179.50 Max. :126.50 Max. :17.00 Max. :96.50
round( cor(da), 3)
chest weight region height
chest 1.000 0.697 0.016 0.255
weight 0.697 1.000 0.023 0.458
region 0.016 0.023 1.000 -0.152
height 0.255 0.458 -0.152 1.000
#
# Let's shorten the names, to study the regression:
C = da$chest; W = da$weight; R = da$region; H = da$height
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5); Point(C,W,"magenta")
LR(C,W)
[1] -15.300034 0.940987
f = function(x) LR(C,W)[1]+LR(C,W)[2]*x; graph1(f,50,200,"black")
# Let's study the inverse relationship, too:
LR(W,C)
[1] 54.9919381 0.5170087
g = function(y) LR(W,C)[1]+LR(W,C)[2]*y
# We must represent the inverse relation (x <-> y).
# We represent it as CURVE instead of function
G = function(x,y) x - g(y); CUR(G,"seagreen")
POINT(mean(C),mean(W),"blue")
 # If we have a large numbers of points we can use more or less dense colors according
# to the frequency. We have two chances. The first (picture in the middle):
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, Dcol(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown"); POINT(mean(C),mean(W),"red")
# The second (picture on the right)
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, DCOL(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown")
#
# Let's see the histograms of height and weight, too:
dev.new(); hist(H,right=FALSE,probability=TRUE,col="grey");BOX()
dev.new(); hist(W,right=FALSE,probability=TRUE,col="grey");BOX()
# If we have a large numbers of points we can use more or less dense colors according
# to the frequency. We have two chances. The first (picture in the middle):
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, Dcol(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown"); POINT(mean(C),mean(W),"red")
# The second (picture on the right)
Plane(min(C)-5,max(C)+5, min(W)-5,max(W)+5)
Point(C,W, DCOL(C,W) )
graph1(f,50,200,"black"); CUR(G,"brown")
#
# Let's see the histograms of height and weight, too:
dev.new(); hist(H,right=FALSE,probability=TRUE,col="grey");BOX()
dev.new(); hist(W,right=FALSE,probability=TRUE,col="grey");BOX()
 # The histogram of chest is hampered by not reliable data.
# Well, I cut off the tails:
dev.new(); hist(C,right=FALSE,probability=TRUE,col="grey");BOX()
C2=0; for(i in 1:4140) C2[i]=C1[i+15]
dev.new(); hist(C2,nclass=15,right=FALSE,probability=TRUE,col="grey");BOX()
# The histogram of chest is hampered by not reliable data.
# Well, I cut off the tails:
dev.new(); hist(C,right=FALSE,probability=TRUE,col="grey");BOX()
C2=0; for(i in 1:4140) C2[i]=C1[i+15]
dev.new(); hist(C2,nclass=15,right=FALSE,probability=TRUE,col="grey");BOX()
 # ---------- ---------- ---------- ----------
# QQ plot (quantiles against quantiles plot) is an instrument sometimes employed to
# compare distributions.
# An example of use (referring to the previuos data).
HP=0; for(i in 1:19) HP[i] = Percentile(H,i*5)
WP=0; for(i in 1:19) WP[i] = Percentile(W,i*5)
CP=0; for(i in 1:19) CP[i] = Percentile(C,i*5)
# Some percentiles of the variables and their graphic comparison:
PlaneP(HP,WP); Point(HP,WP,"brown"); abovex("H");abovey("W")
PlaneP(HP,CP); Point(HP,CP,"brown"); abovex("H");abovey("C")
PlaneP(WP,CP); Point(WP,CP,"brown"); abovex("W");abovey("C")
# ---------- ---------- ---------- ----------
# QQ plot (quantiles against quantiles plot) is an instrument sometimes employed to
# compare distributions.
# An example of use (referring to the previuos data).
HP=0; for(i in 1:19) HP[i] = Percentile(H,i*5)
WP=0; for(i in 1:19) WP[i] = Percentile(W,i*5)
CP=0; for(i in 1:19) CP[i] = Percentile(C,i*5)
# Some percentiles of the variables and their graphic comparison:
PlaneP(HP,WP); Point(HP,WP,"brown"); abovex("H");abovey("W")
PlaneP(HP,CP); Point(HP,CP,"brown"); abovex("H");abovey("C")
PlaneP(WP,CP); Point(WP,CP,"brown"); abovex("W");abovey("C")
 # As we have seen (better) comparing the histograms, I find that W and C have a
# similar distribution.
# ---------- ---------- ---------- ----------
# Still something about the study of the relation between two variables.
# As we have seen (better) comparing the histograms, I find that W and C have a
# similar distribution.
# ---------- ---------- ---------- ----------
# Still something about the study of the relation between two variables.

 # F = k·H, 18.240 ≤ k ≤ 19.325, or k = 18.8±0.6
#
# If I don't know the precision of the measurements I can proceed as we saw just above:
Plane(0,60, 0,1000); POINT(H,F, "brown"); abovex("H"); abovey("F")
LR(H,F) # if I don't know that for H=0 F=0
# -21.40182 19.25085
f = function(x) LR(H,F)[1]+LR(H,F)[2]*x; graph1(f,0,60,"red")
LR0(H,F, 0,0) # if I know that for H=0 F=0
# 0 18.69485 <- LR01 LR02 y=LR01+LR02*x
g = function(x) LR02*x; graph1(g,0,60,"seagreen")
# F = k·H, 18.240 ≤ k ≤ 19.325, or k = 18.8±0.6
#
# If I don't know the precision of the measurements I can proceed as we saw just above:
Plane(0,60, 0,1000); POINT(H,F, "brown"); abovex("H"); abovey("F")
LR(H,F) # if I don't know that for H=0 F=0
# -21.40182 19.25085
f = function(x) LR(H,F)[1]+LR(H,F)[2]*x; graph1(f,0,60,"red")
LR0(H,F, 0,0) # if I know that for H=0 F=0
# 0 18.69485 <- LR01 LR02 y=LR01+LR02*x
g = function(x) LR02*x; graph1(g,0,60,"seagreen")
 # To evaluate the goodness of approximation obtained with the regression line, I
# proceed as follows, in the first case (LR): (F function of H; first F, then H)
confInt(F,H, 90/100)
# 5 % 95 %
# (Intercept) -90.15108 47.34745
# Conf 17.27649 21.22522
# In the second case (LR0):
confInt0(F,H, 0,0, 90/100)
# 5 % 95 %
# Conf 18.03658 19.35311 (quite similar to 18.240 19.325)
# These are the confidence intervals at the 90% (0.9) significance level of the slope
# and (in the first case) of the intercept of the line. I can change the level.
# To evaluate the goodness of approximation obtained with the regression line, I
# proceed as follows, in the first case (LR): (F function of H; first F, then H)
confInt(F,H, 90/100)
# 5 % 95 %
# (Intercept) -90.15108 47.34745
# Conf 17.27649 21.22522
# In the second case (LR0):
confInt0(F,H, 0,0, 90/100)
# 5 % 95 %
# Conf 18.03658 19.35311 (quite similar to 18.240 19.325)
# These are the confidence intervals at the 90% (0.9) significance level of the slope
# and (in the first case) of the intercept of the line. I can change the level.
 # H and F are strongly correlated (see above):
cor(H,F)
# 0.9987686 (about 1)
# To value the efficacy of the correlation we determine a confidence interval
cor.test(H,F, conf.level=0.90)
# 90 percent confidence interval:
# 0.9674734 0.9999541 (comments on the other outputs)
# Another correlation coefficient often used is "Sperman's". It is indicated with ρ (the
# Greek letter "ro", which corresponds to our R) in that it compares the "ranks" of the
# data, ie not their values but their order number (1st, 2nd, ...). See here. An example:
x = c(10,20,30,40); y = c(15,60,70,200)
cor(x,y); cor(x,y, method="spearman")
# 0.9173057 1
# The data is arranged in an increasing way, but not aligned. The usual correlation
# coefficient is close to 1. The Spearman coefficient is instead just 1, indicating that
# the data is increasing, beyond the way they grow. Another example:
x = c(10,20,30,40,50); y = c(1,2,-900,3,4)
cor(x,y); cor(x,y, method="spearman")
# 0.002742232 0.7
# ---------- ---------- ---------- ----------
# For linear, quadratic and cubic regression and for spline see here
# ---------- ---------- ---------- ----------
# The coefficient of correlation can be found also for other type of function. An example.
# We can define:
COR2 = function(X,Y,f) {Sr=sum((y-f(x))^2);Sm=sum((Y-mean(Y))^2);sqrt((Sm-Sr)/Sm)}
# Or we can use the already defined function cor2
# We want compare the following data with the quadratic regression
x <- c(0,1,2,3,4,5); y <- c(2.1,7.7,13.6,27.2,40.9,61.1)
Plane(-1,6, 0,70); POINT(x,y, "blue")
regression2(x,y)
# 1.86 * x^2 + 2.36 * x + 2.48
f=function(x) 1.86 * x^2 + 2.36 * x + 2.48; graph1(f,-1,6, "black")
cor2(x,y,f)
# 0.9992544 A value near to 1! With linear regression I have:
cor(x,y)
# 0.9731813
# I can obtain the same value with cor2 if I put this function:
regression1(x,y)
# 11.66 * x + -3.724
g = function(x) 11.66 * x + -3.724; graph1(g,-1,6, "red")
cor2(x,y,g)
# 0.9731812
# H and F are strongly correlated (see above):
cor(H,F)
# 0.9987686 (about 1)
# To value the efficacy of the correlation we determine a confidence interval
cor.test(H,F, conf.level=0.90)
# 90 percent confidence interval:
# 0.9674734 0.9999541 (comments on the other outputs)
# Another correlation coefficient often used is "Sperman's". It is indicated with ρ (the
# Greek letter "ro", which corresponds to our R) in that it compares the "ranks" of the
# data, ie not their values but their order number (1st, 2nd, ...). See here. An example:
x = c(10,20,30,40); y = c(15,60,70,200)
cor(x,y); cor(x,y, method="spearman")
# 0.9173057 1
# The data is arranged in an increasing way, but not aligned. The usual correlation
# coefficient is close to 1. The Spearman coefficient is instead just 1, indicating that
# the data is increasing, beyond the way they grow. Another example:
x = c(10,20,30,40,50); y = c(1,2,-900,3,4)
cor(x,y); cor(x,y, method="spearman")
# 0.002742232 0.7
# ---------- ---------- ---------- ----------
# For linear, quadratic and cubic regression and for spline see here
# ---------- ---------- ---------- ----------
# The coefficient of correlation can be found also for other type of function. An example.
# We can define:
COR2 = function(X,Y,f) {Sr=sum((y-f(x))^2);Sm=sum((Y-mean(Y))^2);sqrt((Sm-Sr)/Sm)}
# Or we can use the already defined function cor2
# We want compare the following data with the quadratic regression
x <- c(0,1,2,3,4,5); y <- c(2.1,7.7,13.6,27.2,40.9,61.1)
Plane(-1,6, 0,70); POINT(x,y, "blue")
regression2(x,y)
# 1.86 * x^2 + 2.36 * x + 2.48
f=function(x) 1.86 * x^2 + 2.36 * x + 2.48; graph1(f,-1,6, "black")
cor2(x,y,f)
# 0.9992544 A value near to 1! With linear regression I have:
cor(x,y)
# 0.9731813
# I can obtain the same value with cor2 if I put this function:
regression1(x,y)
# 11.66 * x + -3.724
g = function(x) 11.66 * x + -3.724; graph1(g,-1,6, "red")
cor2(x,y,g)
# 0.9731812

 # But math is not enough! In the case of the picture on the right:
x <- c(0,1,2,3,4,5); y <- c(2,19,38,15,48,43)
Plane(-1,6, 0,50); POINT(x,y,"black")
regression1(x,y) # 7.686 * x + 8.286
f1=function(x) 7.686 * x + 8.286; graph1(f1,-1,6, "blue")
regression2(x,y) # -0.964 * x^2 + 12.5 * x + 5.07
f2=function(x) -0.964 * x^2 + 12.5 * x + 5.07; graph1(f2,-1,6, "brown")
regression3(x,y) # 0.87 * x^3 + -7.49 * x^2 + 24.4 * x + 2.46
f3=function(x) 0.87*x^3-7.49*x^2+24.4*x+2.46; graph1(f3,-1,6, "red")
cor2(x,y,f1); cor2(x,y,f2); cor2(x,y,f3)
# 0.7916388 0.8048205 0.8230846
# The cubic function gives a better correlation. But the type of function (a polynomial
# or other function) with which I can approximate the data depends on the context.
# But math is not enough! In the case of the picture on the right:
x <- c(0,1,2,3,4,5); y <- c(2,19,38,15,48,43)
Plane(-1,6, 0,50); POINT(x,y,"black")
regression1(x,y) # 7.686 * x + 8.286
f1=function(x) 7.686 * x + 8.286; graph1(f1,-1,6, "blue")
regression2(x,y) # -0.964 * x^2 + 12.5 * x + 5.07
f2=function(x) -0.964 * x^2 + 12.5 * x + 5.07; graph1(f2,-1,6, "brown")
regression3(x,y) # 0.87 * x^3 + -7.49 * x^2 + 24.4 * x + 2.46
f3=function(x) 0.87*x^3-7.49*x^2+24.4*x+2.46; graph1(f3,-1,6, "red")
cor2(x,y,f1); cor2(x,y,f2); cor2(x,y,f3)
# 0.7916388 0.8048205 0.8230846
# The cubic function gives a better correlation. But the type of function (a polynomial
# or other function) with which I can approximate the data depends on the context.
