Esempi introduttiviI limiti in probabilità [1ª parte] (2ª)
Esempi introduttivi
 |
Abbiamo visto
( leggi di distribuzione - var. discrete)
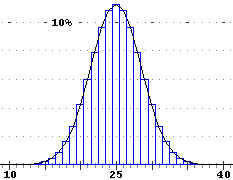
che il grafico della legge binomiale Bn,p
(di ordine n e "probabilità di successo nella singola prova" p) quando n cresce
tende ad assumere una particolare forma (a lato il grafico di |
||
| Vi sono altre variabili casuali che rappresentano la ripetizione di esperimenti e che all'aumentare del numero degli esperimenti tendono ad avere una legge di distribuzione il cui grafico tende ad assumere tale forma: | |||
|
| • Se dalla somma di due variabili con distribuzione uniforme passo al caso in cui gli addendi sono quattro, da un istogramma dalla forma triangolare (vedi sopra) passo ad uno come quello sotto a sinistra (è il lancio di 4 dadi equi). |
| • Sotto a destra è rappresentata una situazione analoga, in cui gli addendi sono stati aumentati a 12. |
tot<-10000; x<-vector(length=tot)
for (i in 1:tot) { x[i] <- 0; for (j in 1:4)
x[i] <- x[i]+floor(runif(1)*6)+1 }
hist(x,seq(4-1/2,6*4+1/2,1),right=FALSE,freq=FALSE)
for (i in 1:tot) { x[i] <- 0; for (j in 1:12)
x[i] <- x[i]+floor(runif(1)*6)+1 }
hist(x,seq(12-1/2,6*12+1/2,1),right=FALSE,freq=FALSE) |
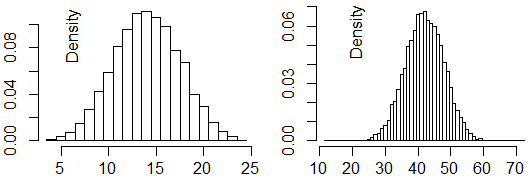
• Qui trovi altri esempi, relativi alla somma di altri tipi di variabili casuali, non distribuite uniformemente, e anche in tutti questi casi trovi che all'aumentare delle variabili sommate le frequenze delle uscite tendono a distribuirsi formando un istogramma dalla forma a campana.
Nota. Vengono spesso usati i termini statistica descrittiva e statistica induttiva (o statistica inferenziale) per indicare, rispettivamente, la parte della matematica che si occupa della raccolta e della descrizione di una serie di dati su certi fenomeni e quella che si occupa della rappresentazione dei fenomeni stessi mediante dei modelli matematici che cercano di descriverne il comportamento nel caso astratto, in cui si diponesse di tutti i dati raccoglibili. La statistica inferenziale, dunque, mette insieme gli stumenti utilizzati dalla statistica descrittiva con quelli messi a punto per affrontare il calcolo delle probabilità. Questo collegamento tra i dati osservati e la loro rappresentazione mediante opportuni modelli matematici astratti è l'oggetto di studio di questa voce degli Oggetti Matematici.
Il teorema limite centrale
Queste osservazioni e congetture possono essere precisate:
Siano Ui (i intero positivo) variabili casuali (numeriche) indipendenti con la stessa legge di
distribuzione. La variabile casuale
|
Precisando ulteriormente, si ha che, comunque si fissi h, tende a 0 per n → ∞ l'errore che si commette sostituendo Yn a Xn nel calcolo della probabilità che l'uscita cada in un qualunque intervallo di ampiezza h.
Se le Ui hanno |
 |
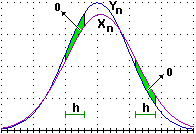La proprietà descritta in questo paragrafo è nota come teorema limite centrale.
È assai importante, in quanto consente di concludere che la media di una serie di rilevamenti di una qualunque
grandezza (non i rilevamenti stessi!) ha andamento gaussiano. Su ciò torneremo fra un paio di paragrafi.
Ne esiste anche una versione più "forte",
che si estende a situazioni in cui le variabili casuali sommate non hanno la stessa legge di distribuzione
( vedi),
e che consente di capire perché vi siano svariate grandezze di natura biologica le cui misure hanno andamento gaussiano.
Le proprietà della gaussiana
Abbiamo già
messo a fuoco varie proprietà della gaussiana
leggi di distribuzione - var. continue).
Si può congetturare su vari esempi
prova)
Dalla media statistica alla media teorica
Facciamo un esempio.
Se vogliamo determinare il peso medio della popolazione adulta (di un certo paese) di un dato sesso,
ad es. maschile,
possiamo rilevare i pesi P1, P2,
..., Pn di n persone e farne la media
Se P è la variabile casuale "peso di un abitante adulto maschile", possiamo scrivere
Le Pi sono
tutte variabili casuali distribuite come P (se prendo le persone in
modo del tutto casuale); se faccio i rilevamenti in modo indipendente, per il teorema limite centrale ho che
All'aumentare di n (possiamo dire "per n → ∞",
essendo grande la popolazione rispetto alle quantità
di rilevamenti che vengono effettuati)
lo scarto quadratico medio σ* di questa gaussiana
(uguale allo s.q.m. σ di P diviso per √n) tende a 0, per cui il valore
Ad es., supponendo che P sia espressa in kg, se voglio determinare il peso medio della popolazione a meno di 0.5 kg posso fare tante prove n fino a che σ* = σ/√n < 0.5. A quel punto potrò dire che, con probabilità del 68.3%, il valore
Se voglio una stima più sicura, praticamente certa,
posso fare tante prove n fino a che 3σ* = 3σ/√n < 0.5. A quel punto potrò dire che, con probabilità del 99.7%, il valore
Il valore di σ devo già conoscerlo in base a considerazioni di qualche tipo oppure posso man mano approssimarlo sulla base degli n rilevamenti fatti (vedi due paragrafi avanti).
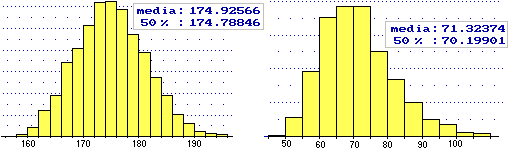
Ricordiamo che sono le medie dei pesi che si misurano ad avere andamento gaussiano, non i pesi stessi. Per confermare questo si considerino gli istogrammi seguenti: quello a sinistra e quello a destra rappresentano la distribuzione, rispettivamente, delle altezze (in cm) e dei pesi (in kg) rilevati alle visite di leva per la Marina del 1997 (primi scaglioni); si tratta di circa 4 mila maschi italiani ventenni. Come si vede, mentre l'istogramma delle altezze ha forma approssimativamente gaussiana, ciò non vale per quello dei pesi.
 |
Ha senso dire che nel 1997 l'uomo |
Convergenza in probabilità e "Legge dei grandi numeri"
Quanto discusso ed esemplificato sopra può essere sintetizzato dicendo che
se U1, …, Un sono n variabili casuali con la stessa legge di distribuzione, con media μ e
scarto quadratico medio σ, allora la loro media, ossia la variabile casuale
[ per il teo. limite centrale:
Pr ( | ΣiUi/n – μ | < ε) → Pr ( | Yn/n – μ | < ε)
per n → ∞
Pr ( | Yn/n – μ | < ε) → 1; infatti (M(Yn/n) = μ e) all'aumentare di n σ(Yn/n) = σ/√n tende a 0.
Quindi ho anche:
Pr ( | ΣiUi/n – μ | < ε) → 1 ]
Il concetto di "limite in probabilità" coincide con quello usuale, a parte il fatto che si trova un valore di n a partire dal quale vale la diseguaglianza non con certezza, ma con una certa probabilità. Ciò corrisponde al fatto che, ad es., se lancio una coppia di dadi prima o poi la media delle uscite si stabilizza attorno a 7, ma, anche se è altamente improbabile, potrebbe accadere che a un certo punto si susseguano 20 uscite uguali a 2 che abbassino, provvisoriamente, la media.
Le considerazioni svolte in questo paragrafo spesso sono descritte medianti proprietà note come leggi dei grandi numeri (e a volte raggruppate sotto la voce legge di Bernoulli in quanto Jakob Bernoulli - intorno al 1700 - ne dette una prima formulazione).
Possiamo a questo punto precisare
perché se si hanno dei dati approssimati alla stessa cifra (unità, decimi, …)
la loro media può essere approssimata alla cifra successiva (decimi, centesimi, …) se i dati sono almeno una decina, alla seconda cifra successiva (centesimi, millesimi, …) se sono almeno un migliaio, alla terza cifra successiva (millesimi, decimillesimi, …) se sono almeno un centinaio di migliaia, … [aggiungendo 1/2 unità corrispondente alle
cifre finali dei dati originali se questi erano troncati].
Infatti i dati approssimati x1,...,xn differiscono dal
dato esatto per errori ei che cadono in un intervallo ampio u
(u=1 se le approssimazioni sono agli interi, u=0.1 se sono ai decimi, ...).
Nel fare la media,
Quindi, quando vogliamo trovare il valor medio relativo ad un certo aspetto di una data popolazione di soggetti attraverso una
indagine statistica, la numerosità del campione, all'aumentare della numerosità della popolazione dei soggetti indagati,
deve crescere meno velocemente di questa: se per una certa indagine su una popolazione di 1000 soggetti usiamo un campione di 50 soggetti e se
vogliamo svolgere un'indagine analoga con esiti confrontabili su una popolazione di 9000 soggetti, dato che √9 = 3, dobbiamo utilizzare
un campione di 50·3 soggetti.
L'ultima cifra della media così approssimata può differire di una o due unità dalla corrispondente cifra del valore che si sarebbe ottenuto approssimando i dati originali. Per avanzare di un posto nella approssimazione "avendo tutte le cifre buone" avremmo dovuto prendere non 10 ma 100 dati, e quindi una decina di migliaia, un milione, ... di dati per prendere due, tre, ... cifre in più rispetto ai dati originali.
Infatti se i dati sono approssimati alla cifra di unità u, la media può essere arrotondata a una cifra in più se l'errore è al massimo mezza dell'unità 10 volte più piccola, ossia 0.05u. Gli ei si disperdono uniformemente su un intervallo ampio u; il loro s.q.m. è σ = u/√12 e lo s.q.m. dell'errore medio se n=100 è σ* = u/√12/√n = u/√1200 = 0.029u: al 68% l'errore è al più 0.029u, al 95% è al più 2σ* = 0.058u; quindi è molto alta (91%, come si può verificare) la probabilità che la cifra in più sia buona. Con probabilità 99.7% è al più 3σ* = 0.087u < u/10, quindi è praticamente certo che l'errore non superi un'unità sull'ultima cifra.
Stima non distorta di σ
Abbiamo visto che per il teorema limite centrale, data una variabile casuale X, la media statistica Mn(X)
(ossia la variabile casuale ottenuta come media aritmetica di n esperimenti, cioè dei valori assunti da n variabili casuali distribuite come X)
all'aumentare di n tende a comportarsi come M(X), e che quindi può essere assunta come stima di essa
ed usarla al suo posto per vari scopi pratici.
Supponiamo che n sia piccolo. Fisso ad es. n=10.
Se calcolo ripetutamente
Posso anche prendere lo scarto quadratico medio di
Se fisso n, ad es. n=10, e calcolo ripetutamente la varianza di prova
In generale si domostra che, fissato n, la varianza di
Per questo motivo alla media statistica
√(Σ(datoi-media)2/n) · √(n/(n-1)) = √( Σ(datoi – media)2 / (n-1) )
Naturalmente se n è grande i due valori sono praticamente coincidenti: 999/1000 = 0.999 = 1-0.001 (differenza dello 0.1%).
Una giustificazione "pratico-intuitiva" per l'uso di
Nota. A volte,
specie sulle calcolatrici, mentre lo scarto quadratico medio statistico viene indicato σn, lo stimatore non distorto viene indicato
Spesso si usa deviazione standard della "variabile casuale" X al posto
di scarto quadratico medio (teorico)
di X e, dato un rilevamento statistico, viene chiamata deviazione standard statistica, o campionaria,
lo stimatore corretto e non distorto dello scarto quadratico medio teorico.
Data una distribuzione statistica Y di N dati viene spesso chiamata
deviazione standard di Y, e
indicata con
A volte, però, con deviazione standard statistica viene indicato lo s.q.m. statistico
(stimatore corretto ma distorto). Vedi 
più avanti per la deviazione standard della media.
I limiti in probabilità (2ª parte)
Probabilità di eventi mediante simulazione
La legge dei grandi numeri giustifica il procedimento sperimentale per la determinazione delle probabilità
Infatti, detto K il numero delle volte che si verifica l'evento E in n prove indipendenti, abbiamo che K/n (=ΣiVi/n, Vi distribuiti come V così definita: V=1 se E è vero, V=0 altrimenti) converge a Pr(E) = M(V), e sappiamo come si distribuisce: è approssimabile con la gaussiana di media Pr(E) e s.q.m. σ(V)/√n. Quindi possiamo valutare la probabilità con cui K/n cade in certo intervallo.
Lo script o i programmi in R (a cui
da qui ci si può collegare) traduce questo procedimento:
• ripetere l'esperimento più volte e calcolare man mano la frequenza relativa Fr di successo (cioè ΣiVi/n);
• man mano calcolare lo s.q.m. statistico S di V, che approssima σ(V) (il programma prende Fr(1–Fr) come approssimazione della varianza teorica Pr(E)(1-Pr(E)) essendo V una binomiale);
• calcolare Sn= S/√(n-1), come approssimazione dello s.q.m. teorico di ΣiVi/n;
• calcolare Fr – 3·Sn e Fr + 3·Sn, che sono interpretabili come gli estremi dell'intervallo in cui, al 99.7%, cade Pr(E).
Nota 1. Si usa dire che all'intervallo frequenza
Nota 2.
Come trovare il t della nota precedente (chiamato coefficiente fiduciario) a cui corrisponde una data probabilità di confidenza? Possiamo
usare un semplice programmino che, data la
distribuzione normale - o gaussiana - standard G (abbiamo visto che basta riferirsi a quella
di media 0 e sc.quad.medio 1), alla probabilità P associa h tale che
dn <- function(x) dnorm(x, mean=0, sd=1 )
integrate(dn,-1,1)$value
# 0.6826895 ritrovo il valore visto sopra
# Ora dato P cerco h tale che valga la relazione considerata sopra:
idn <- function(x) integrate(dn,-x,x)$value-P
P <- 0.9; uniroot( idn,c(-100,100))$root
# 1.644864
P <- 0.95; uniroot( idn,c(-100,100))$root
# 1.959952
P <- 0.99; uniroot( idn,c(-100,100))$root
# 2.575827
P <- 0.999; uniroot( idn,c(-100,100))$root
# 3.290527
P <- 0.6826895; uniroot( idn,c(-100,100))$root
# 1.000006
Quindi la probabilità di confidenza del 99% è associata all'intervallo
Misurazioni ad alta sensibilità
Un cronometro (o un comune orologio al quarzo di tipo digitale) che visualizza i centesimi di secondo è uno strumento a bassa sensibilità
calcolo
Analogamente, se si usa un doppio decimetro per misurare la lunghezza L di un oggetto, si individua la tacca più vicina alla estremità dell'oggetto e, se ad es. questa rappresenta 13.4 cm, si prende 13.4 cm±1/2 mm come approssimazione certa di L, cioè [13.35,13.45] come intervallo di indeterminazione per il valore (in cm) di L.
Per fare un esempio semplice ma reale di misurazione ad alta sensibilità consideriamo un reflettometro per la determinazione del tasso glicemico del sangue (viene depositata una goccia di sangue su una striscetta, che viene inserita nello strumento; questo, mediante un opportuno dispositivo ottico, effettua il rilevamento ed esprime il valore in mg/dl). In dotazione è presente (per verificare il corretto funzionamento dell'apparecchio) una striscia di controllo trattata in modo da avere caratteristiche corrispondenti a quelle di una goccia di sangue con un certo tasso glicemico.
| Se ripeto più volte la misurazione del "tasso glicemico" della striscia di controllo non ottengo sempre lo stesso valore. A destra è riprodotto l'istogramma relativo a 89 rilevamenti. |  |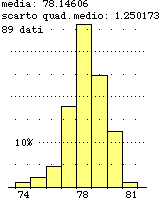
||
 |
Le variazioni tra un rilevamento e l'altro sono dovute a una serie di fattori casuali (in cui intervengono aspetti ottici, elettronici, …) che non è possibile né eliminare né conoscere esattamente, per cui il valore letto è da interpretare come una variabile casuale. Aumentando le prove l'istogramma
si stabilizza sulla rappresentazione della legge di distribuzione;
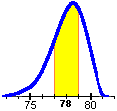
i centri delle sue basi superiori potrebbero collocarsi su una curva simile a quella a sinistra. Come faccio a decidere in che modo approssimare la misura ottenta? | ||
|
Nel caso della striscia di controllo, sottoposta a quasi un centinaio di rilevamenti, posso dire che il valore medio (o valore "atteso")
è 78.1. Con più precisione che è 78.146...±3·1.25.../√88 (con probabilità del 99.7%), cioè 78.14±0.40 (mg/dl)
(vedi qui per l'elaborazione dei dati). Ma non è detto che questo sia il valore vero del tasso glicemico della striscia di controllo, è solo il valore atteso della variabile casuale "esito di un rilevamento per la striscia di controllo". | |||
Posso comunque osservare che l'istogramma, pur avendo una "coda" a sinistra, ha forma quasi simmetrica, e ipotizzare quindi che gli errori casuali siano sia positivi che negativi e che le misure rilevate tendano a cadere attorno alla misura "vera", e posso supporre che questa sia "circa" (a meno di 1 unità) 78 (vedi parte colorata sul grafico sopra a sinistra).
Se faccio un rilevamento per una certa persona non ha senso effettuare molte prove e calcolare il valor medio: in brevi intervalli di tempo il tasso può cambiare (per cui ripetendo la prova non è detto che si effettui sempre la misurazione della stessa grandezza) e, poi, non interessano valutazioni molto precise. Tenendo conto dello studio effettuato sulla striscia di controllo possiamo stimare in circa 5 unità lo scarto che il valore letto può avere dal valore vero e associare alla misura letta tale precisione: se leggo 93, assumo che il tasso glicemico sia 93±5 mg/dl.
Consideriamo una misurazione ad alta sensibilità per cui abbia
invece senso effettuare più rilevamenti.
Un cronometro (o un comune orologio al quarzo di tipo digitale) che visualizza i centesimi di secondo è uno strumento a bassa sensibilità: se venisse avviato e arrestato il cronometro più volte, facendo trascorrere sempre lo stesso tempo T tra l'avvio e l'arresto, sul visore si leggerebbe sempre lo stesso tempo. Se ad esempio si leggesse 3.27 vorrebbe dire che T è compreso tra 3.27 sec e 3.28 sec, cioè che [3.27,3.28] è un intervallo di indeterminazione "certo" per la misura di T in secondi.
Ma se il cronometro è azionato manualmente, misurando sempre lo stesso intervallo di tempo si possono ottenere valori diversi. Ad esempio se avvio e arresto la misurazione man mano che un altro orologio scatta di 1 sec, non troverò, in genere, esattamente 1 sec, ma potrò trovare, via via che ripeto la misurazione, 1.06, 59.93, 59.99, 1.04, 59.95,
Nel file
t-sec.txt sono registrati i 47 valori in centesimi
di secondo ottenuti da una persona misurando manualmente con un orologio il tempo che impiega un altro orologio a scattare in avanti
di 1 s. La misura vera è quindi
tempi <- scan("http://macosa.dima.unige.it/R/t-sec.txt", skip=1)
str(tempi)
# num [1:47] 111 103 109 97 99 110 99 103 109 106 ...
summary(tempi)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.00 96.00 98.00 99.36 107.50 129.00
99.36 è molto inferiore a 100. Dobbiamo osservare che le misure ottenute con l'orologio
sono troncate ai centesimi di secondo. Correggiamo quindi i dati con
tempi <- tempi+1/2 valori
 |
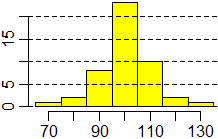Min. 1st Qu. Median Mean 3rd Qu. Max. 68.50 96.50 98.50 99.86 108.00 129.50 hist(tempi,right=FALSE,col="yellow",seq(65,135,10)) abline(h=axTicks(2),lty=2) |
L'istogramma è abbastanza simmetrico. E, in effetti, ha senso ritenere che il rilevamento manuale dia luogo a scostamenti positivi e negativi dal valore "vero" che si compensano. Aumentando il numero dei rilevamenti vedremmo più chiaramente questa simmetria.
Nell'ipotesi che le misure si distribuiscano in modo tendenzialmente simmetrico intorno alla misura vera, possiamo assumere la media come stima della misura vera (infatti se la funzione densità ha grafico simmetrico, l'asse di simmetria deve intersecare l'asse orizzontale in corrispondenza della media).
Come valutare la precisione con cui la media approssima la misura vera?
Procediamo come abbiamo fatto prima per la misura attesa della striscia di controllo, tenendo conto che ora assumiamo che misura attesa e misura vera coincidano: stimiamo lo s.q.m. teorico con σ* = σ/√46, essendo σ quello sperimentale; facendo il calcolo con R [sd(tempi)/sqrt(length(tempi)): R in "sd" mette la stima "non distorta" delle scarto quadratico medio, per cui poi si divide per √n invece che per √(n-1): vedi la nota del prossimo paragrafo] otteniamo 1.583163, e possiamo determinare la probabilità con cui la misura vera dista dalla media sperimentale meno di t·σ*.
Nel nostro caso, supposto – come è ragionevole fare in questo frangente – che l'apparato non sia affetto da errori sistematici (cioè che l'orologio non vada avanti o indietro in modo significativo e che l'uomo non ritardi sistematicamente una della due pressioni – quella di avvio o quella di arresto – maggiormente dell'altra), possiamo dire, ad esempio, che la misura vera è 99.86±3σ* = 99.86±4.75 (cioè che cade in [95.1,104.6]) al 99.7%. Possiamo dire che (con pratica "certezza") è 100±5 (cs).
Nota. Una stima più grossolana era prendere direttamente l'arrotondamento della media 99.86 a 100 (agli interi, come erano approssimati i dati di partenza) o a 99.9 (±0.2), ossia alla cifra successiva (con un'incertezza di 2 unità) a quella a cui erano approssimati i dati, essendo questi alcune decine.
Tutto questo
(assumere la media come stima della misura vera) vale nell'ipotesi di simmetria attorno
alla misura vera fatta inizialmente, che (come visto per il riflettometro)
non vale in generale.
Supponiamo, ad es., di avere un dispositivo che misuri le velocità di oggetti indirettamente,
rilevando il tempo che l'oggetto impiega per percorrere 1 m. Supponiamo che l'oggetto viaggi esattamente
alla velocità di 1 m/s, che essa sia misurabile più volte e che i tempi rilevati siano quelli
contenuti in t-sec. Il dispositivo ogni volta aggiunge 0.5 centesimi al dato rilevato (in modo da trasformarlo
da troncamento in arrotondamento; vedi sopra) e divide 100 per esso, in modo da ottenere velocità in m/s.
Ecco i "calcoli" con R e gli esiti:
 |
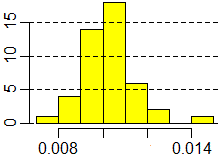Min. 1st Qu. Median Mean 3rd Qu. Max. 0.007722 0.009261 0.010150 0.010140 0.010360 0.014600 |
Si può osservare che l'istogramma è meno simmetrico e che la media ha distanza relativa dal valore vero (1.014 differisce da 1 dell'1%) maggiore rispetto a quanto accadeva per i tempi (99.86 differiva da 100 dello 0.1%). Con più misurazioni avrei l'illusione di ottenere precisioni man mano migliori ma otterrei invece un intervallo di indeterminazione che si stringe attorno a un valore diverso dalla misura vera: la media delle misure rilevate non converge alla misura vera.
Se invece faccio 100/99.86 (100/tempo medio) ho 1.0014, una buona approssimazione della velocità vera. In definitiva, se t1, t2, ..., tn hanno media μ, 100/t1, 100/t2, ..., 100/tn non hanno come media 100/μ.
In conclusione, di fronte a un apparato come quello in questione, si dovrebbe, combinando studi sperimentali e riflessioni teoriche, individuare una legge di distribuzione delle misure e individuare quale variabile statistica, diversa dalla media sperimentale, assumere come stimatore della misura vera.
Nel caso di pochi dati (10 o 20), comunque, anche se l'andamento non è molto simmetrico (ma neanche troppo "asimmetrico"), poiché σ* rimane grande, si può assumere media±3σ* come intervallo di indeterminazione "praticamente certo" della misura vera.
Nota 1. Spesso il valore che qui abbiamo indicato per comodità con
σ*, cioè σ/√n, viene chiamato deviazione
standard della media (il suo quadrato è chiamato varianza della media). Infatti esso è la deviazione
standard (o s.q.m.) a cui tende la deviazione standard della media statistica (teorema limite centrale).
Qualcuno usa invece il termine errore standard, riferendosi al caso delle misurazioni ad alta
sensibilità, ma scorrettamente: si dovrebbe usare errore standard della media
(l'errore standard andrebbe usato per indicare la deviazione standard).
Se X è una distribuzione statistica,
si usa deviazione standard statistica (o campionaria) della media di X per indicare
Come calcolare con con R
s.q.m. e varianza, la varianza e lo s.q.m. statistici
[cioè gli stimatori non distorti
Nota 2.
Quando i dati sono pochi (n < 10) invece al calcolo della deviazione standard della media
σ/√n per valutare meglio gli intervalli di confidenza si ricorre a un particolare
procedimento detto "t di Student" a cui facciamo solo un cenno, ricorrendo al software R
per il calcolo. Supponiamo che 15, 17, 18, 19, 25 siano i pesi in grammi di 5 topini. Voglio trovare con
la fiducia del 95% un intervallo per il valore della media "vera". Abbiamo già visto
che usando la gasussiana
potremmo procedere così:
topi <- c(15,17,18,19,25)
m <- mean(topi); r <- 1.959952*sd(topi)/sqrt(length(topi))
m; r; c(m-r, m+r)
# 18.8 3.30297 15.49703 22.10297
Usando il t-test di Student (per cui si ricorre al comando t.test) abbiamo:
t.test(topi, conf.level = 0.95)
# One Sample t-test
# t = 11.1557, df = 4
# 95 percent confidence interval:
# 14.12105 23.47895
# mean of x
# 18.8
Si ottiene un intervallo leggermente più grande.
La frase "One Sample t-test" si riferisce al fatto che il test di Student è qui usato per studiare
una sola variabile casuale. In modo opportuno può infatti essere usato anche per studiare la relazione
tra due diverse variabili casuali, argomento di cui ci si occupa in una voce successiva.
Senza entrare nei dettagli, osserviamo solo che "df" ha come valore "n−1"
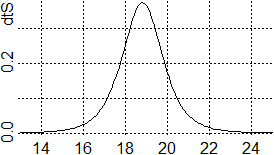
e che il valori 14.1 e 23.5 ottenuti sono gli estremi dell'intervallo (centrato in 18.8) in cui la funzione dtS seguente
(simile alla gaussiana), che rappresenta la distribuzione di t, ha integrale 0.95:
dtS <- function(x) dt(x-18.8,df=4)
plot(dtS,13,25)
abline(h=axTicks(2),v=axTicks(1),lty=3)
Esercizio 3 (soluz.) Esercizio 4 (soluz.) Esercizio 5 (soluz.) Esercizio 6 (soluz.) Esercizio 7 (soluz.) Esercizio 8 (soluz.)
Vedi qui per un uso di R impiegando la libreria
