Regola Pratica

Per la Determinazione dei Massimi e dei Minimi di una Funzione

Il procedimento è schematizzato qui sotto:

[0]    Si deriva la funzione e si trovano gli zeri della derivata prima, cioè si ricercano quegli x tali che f '(x)=0
[1]    Sia x₀ in {x app. a dom(f) / f '(x)=0}; si calcola la derivata seconda f " (x₀). Si possono presentare 3 casi:
        [1.1]    Se f "(x₀)<0, allora x₀ è di massimo relativo per f.
        [1.2]    Se f "(x₀)>0, allora x₀ è di minimo relativo per f.
        [1.3]    Se f "(x₀)=0, allora si calcola la derivata terza f "'(x₀).
[2]   Se f '(x)=f "(x₀)=0 e f "'(x₀)¹0, allora x₀ non è né punto di minimo, né punto di massimo per f.
[3] Se f '(x₀)=f "(x₀)=f "'(x₀)=0, allora si calcolano le derivate successive fino a trovare quella che non si annulla in x₀.
        Sia f ⁽ⁿ⁾(x₀)¹0, la prima derivata che non si annulla in x₀:
        [3.1]     Se n è pari, allora x₀ è punto di estremo relativo per f; in particolare:
                    [3.1.1]    Se f ⁽ⁿ⁾(x₀)>0, allora x₀ è di minimo relativo per f.
                    [3.1.2]    Se f ⁽ⁿ⁾(x₀)<0, allora x₀ è di massimo relativo per f.
        [3.2]     Se n è dispari, allora x₀ non è né punto di minimo, né punto di massimo per f.

Collegamenti

Per i dettagli: Seguire i collegamenti !

[1]

La funzione è stata derivata. Sia x₀ un punto interno al dominio di f tale che f '(x₀)=0. La tangente al grafico in (x₀, f(x₀)) è dunque orizzontale.

Questo tuttavia non significa necessariamente che il punto in questione sia di estremo relativo: potrebbe infatti verificarsi un caso di questo tipo:

Si passa quindi al calcolo della derivata seconda f "(x₀). Si presenterà uno dei 3 casi seguenti:

f "(x₀)<0
f "(x₀)>0
f "(x₀)=0

Torna all'inizio

[1.1]

Il punto x₀ è un punto interno al dominio di f tale che f '(x₀)=0 e f "(x₀)<0. Da tutto ciò si può concludere che x₀ è di MASSIMO relativo per la funzione f

Tutto ciò si può spiegare nel modo seguente:
Siccome f "(x₀)<0, per il teorema della permanenza del segno, esiste allora un intorno I di x₀ in cui f "(x)<0. In tale intorno I, per il corollario 3 al teorema di Lagrange, la funzione f ' sarà strettamente decrescente e dunque, siccome f ' si annulla in x₀, in un intorno sinistro di x₀ la funzione f ' sarà positiva, mentre in un intorno destro f ' sarà negativa.
Le ripercussioni sulla funzione f sono le seguenti: in un intorno sinistro di x₀ la f è strettamente crescente, mentre in un intorno destro la f è strettamente decrescente.
Esiste quindi un intorno di in x₀ cui f(x)<f(x₀).
Il punto x₀ è dunque di massimo relativo per definizione.

Torna all'inizio

[1.2]

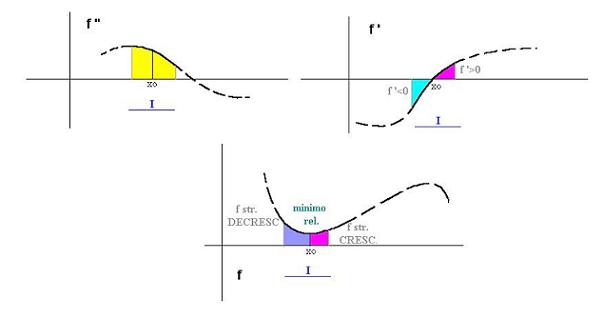
Il punto x₀ è un punto interno al dominio di f tale che f '(x₀)=0 e f "(x₀)>0. Da tutto ciò si può concludere che x₀ è punto di MINIMO relativo per la funzione f

Tutto ciò si può spiegare nel modo seguente:
Siccome f "(x₀)>0, per il teorema della permanenza del segno, esiste allora un intorno I di x₀ in cui f "(x)>0. In tale intorno I, il corollario 3 al teorema di Lagrange, la funzione f ' sarà strettamente crescente e dunque, siccome f ' si annulla in x₀, in un intorno sinistro di x₀ la funzione f ' sarà negativa, mentre in un intorno destro f ' sarà positiva.
Le ripercussioni sulla funzione f sono le seguenti: in un intorno sinistro di x₀ la f è strettamente decrescente, mentre in un intorno destro la f è strettamente crescente.
Esiste quindi un intorno di in x₀ cui f(x)>f(x₀).
Il punto x₀ è dunque di minimo relativo per definizione.

[1.3]

Si ha f '(x₀)=f "(x₀)=0.
Abbiamo quindi le seguenti informazioni su f:

La tangente al grafico di f in (x₀, f(x₀)) è orizzontale.
La tangente al grafico di f ' in (x₀, f ' (x₀))=(x₀, 0) è orizzontale

Non abbiamo però nessun'altra informazione sul comportamento della derivata prima f ': non sappiamo se x₀ è punto di estremo relativo oppure no per la f '.
E' quindi necessario calcolare la derivata terza f "'(x₀). Si possono presentare i seguenti due casi:

f "'(x₀)¹0
f "'(x₀)=0

Torna all'inizio

[2]

Il punto x₀ è un punto interno al dominio di f tale che f '(x₀)= f "(x₀)=0 e f "'(x₀)¹0. Da tutto ciò si può concludere che x₀ NON è NE' punto di MINIMO NE' punto di MASSIMO per la funzione f Infatti, in tal caso, in base a considerazioni precedenti (si vedano [1.1] e [1.2]), possiamo concludere che il punto x₀ risulta essere di estremo relativo per la funzione f '. La situazione è dunque una delle seguenti:

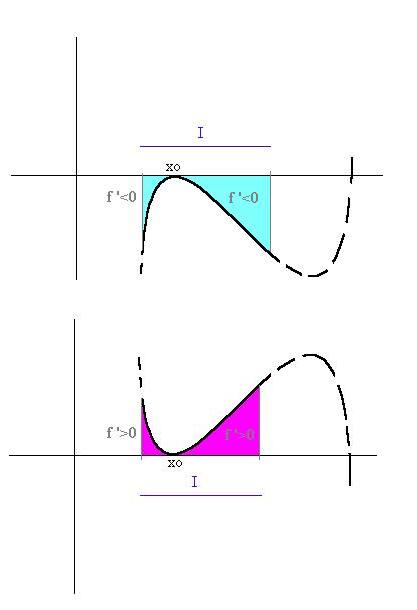Da tutto ciò si può dedurre il comportamento della funzione f:

Nel primo caso, siccome la f ' risulta strettamente negativa in un intorno I di x₀ (eccetto che in x₀), allora nell'intervallo I, per il corollario 3 al teorema di Lagrange, f è strettamente decrescente sia destra che a sinistra di x₀;
Nel secondo caso, simmetricamente, nell'intervallo I, f è strettamente crescente sia destra che a sinistra di x₀.

Le due situazioni sono visualizzate dai seguenti grafici:

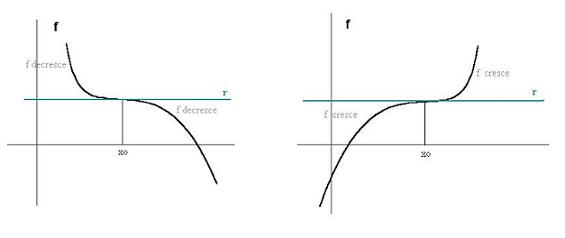Come si può notare, la retta r, tangente al grafico nel punto (x₀, f(x₀)), risulta orizzontale.

Torna all'inizio

[3]

Il punto x₀ è interno al dominio di definizione di f ed è tale che f '(x₀)=f "(x₀)=f "'(x₀)=0. In tal caso si devono calcolare le derivate successive in x₀, fino a trovare quella che non si annulla in x₀.
Sia f ⁽ⁿ⁾(x₀)¹0, la prima derivata che non si annulla in x₀: si possono allora presentare i seguenti casi: