codice). In una successiva voce, calcolatore (5), saranno approfonditi alcuni aspetti relativi alla realizzazione di rappresentazioni grafiche e alla memorizzazione delle informazioni (file e variabili indiciate).Calcolatore (4) - Digitalizzazione
In molte voci abbiamo visto usi del computer per elaborare numeri e informazioni scritte e per elaborare immagini (grafici di funzioni, trasformazioni geometriche, …). Abbiamo anche visto come con un linguaggio di programmazione si possono realizzare programmi che eseguano elaborazioni del primo tipo (usando opportune istruzioni di input e output, variabili numeriche e variabili stringa,
funzioni predefinite, …). Per affrontare il problema di come sono realizzate le applicazioni che producono immagini (da figure
geometriche a "cartoni animati") e suoni (dal "beep"
a brani musicali) approfondiremo lo
studio dei segnali ( codice). In una successiva voce, calcolatore (5), saranno approfonditi alcuni aspetti relativi alla realizzazione di rappresentazioni grafiche e alla memorizzazione delle informazioni (file e variabili indiciate).
Segnali analogici e segnali digitali
Ascoltando
un brano musicale non lo percepiamo come una
messaggio costituito da una sequenza di 
segnali digitali, come,
invece, accade per un messaggio in codice Morse (beep, beeeep,
beeeep, beep, …). Eppure si parla anche di musica
digitalizzata. Perché?
Il
suono può essere descritto come una massa d'aria (o di
altri mezzi, ad esempio acqua) che oscilla e propaga questa
oscillazione nello spazio. Per un'analogia si pensi a due persone,
A e B, che tengano per i due
capi una corda (figura
sottostante): ogni volta che A muove rapidamente, in su e in giù,
la mano, sulla corda si forma un'onda che si sposta fino ad
arrivare alla mano di B, che percepisce un impulso che tende a fargli
muovere la mano. La corda non avanza, ma, comunque, trasmette
dell'energia meccanica. Un fenomeno simile è quello delle onde
del mare.
Consideriamo ad esempio un tamburo: un colpo sulla membrana
la fa oscillare; ogni oscillazione della membrana genera
un'oscillazione nello strato d'aria immediatamente vicino, il quale a
sua volta genera un'oscillazione in un successivo strato d'aria, e
così via. Queste oscillazioni che si propagano nello spazio
vengono dette onde sonore. A differenza dal caso della corda,
che oscilla verticalmente, in su e in giù, perpendicolarmente
alla direzione di avanzamento, nel caso del suono gli strati d'aria
oscillano avanti e indietro, nella stessa direzione in cui avanzano
le onde.
Le
onde sonore che costituiscono la voce umana sono provocate dalle
corde vocali, cioè da due legamenti, posizionati più
o meno all'altezza del pomo d'Adamo, che, chiudendo e aprendo
ripetutamente la laringe, fanno variare il flusso d'aria che esce.
Come
udiamo? Le onde d'aria (o d'acqua se fossimo immersi in mare)
che ci arrivano fanno oscillare la membrana del nostro orecchio
(timpano) con gli stessi intervalli di tempo tra un'oscillazione e la
successiva che avevano in origine (ad es. con gli stessi intervalli
di tempo che vi erano tra le vibrazioni del tamburo o tra le chiusure
della laringe da parte delle corde vocali).
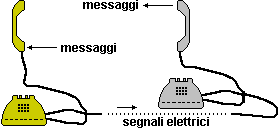
Nel
caso delle conversazioni al telefono i messaggi orali vengono
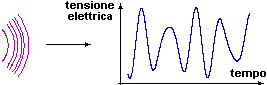
trasformati in segnali elettrici: il
trasmettitore (la parte della cornetta in cui si parla) è
dotato di una membrana che, come il nostro timpano, oscilla sotto la
pressione delle onde sonore; vi è poi un dispositivo che al
variare della posizione della membrana fa variare la tensione
della corrente elettrica che circola in uno dei due fili passanti
per il cavo; in
questo modo le onde sonore vengono trasformate in onde elettriche.
Il ricevitore (la parte della cornetta da cui si ascolta) è
dotato anch'esso di una membrana. In questo caso interviene un
dispositivo che, al variare della tensione della corrente elettrica
che arriva dall'altro filo del cavo, fa oscillare con gli stessi
intervalli di tempo la membrana producendo onde sonore.
|
Nella trasformazione dei segnali digitali in segnali
elettrici la tensione assume solo
un insieme fissato di valori, e
il suo grafico in funzione del tempo ha un
andamento a scatti: la figura a lato è riferita alla
rappresentazione di segnali Morse. Man mano che trascorre un
millisecondo la tensione cambia. La tensione V1
rappresenta "punto"; la tensione V2
rappresenta "linea". Il grafico corrisponde, quindi, a |  |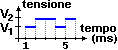
La figura seguente presenta vari esempi di rappresentazioni: (A) di una temperatura, (B) di un brano musicale (un pezzo di spartito e il grafico del segnale elettrico - tensione al variare del tempo - che corrisponde a una esecuzione dello stesso pezzo con un particolare strumento musicale), (C) della rotazione di un certo oggetto (mediante due diversi tipi di contagiri).
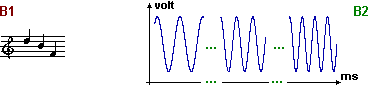
I segnali A1, B1 e C1 sono costituiti da simboli disposti in
modi opportuni, cioè sono segnali digitali (anche la scrittura della musica su uno
spartito
è di tipo digitale: si impiega un insieme finito di simboli
che vengono posti uno a destra dell'altro, a una quota scelta tra un
numero finito di quote possibili, che rappresentano le note; rappresentando le
varie quote, ad esempio, con dei numeri interi potremmo ricondurci a
una sequenza di simboli concatenati sulla stessa riga).
| È digitale anche il codice a barre che è presente sui prodotti in vendita in supermercati, farmacie,… e che viene letto con penne ottiche o altri dispositivi collegati alle casse e a calcolatori che tengono aggiornata la contabilità della merce venduta e presente. Non è altro che una particolare codifica dei numeri con cui sono classificati i vari prodotti (quando il dispositivo ottico non riesce a leggere il codice, il cassiere introduce direttamente i numeri mediante la tastiera). |  |
I
segnali A2, B2, C2 appaiono come fenomeni fisici (una colonnina
di mercurio che cambia lunghezza, il variare di
una tensione elettrica, un indice che scorre lungo un'asta graduata)
che variano con continuità, senza scatti:
osservando la temperatura ambientale indicata in forma digitale mediante
un'insegna al neon o la temperatura corporea indicata da un termometro a lettura
digitale, spesso capita una situazione di instabilità: la
misura visualizzata salta ripetutamente da un valore all'altro, ad
esempio passa da 16° a 17°, poi a 16°, poi a 17°, …;
ciò accade se la temperatura è a metà strada tra
16° e 17° e subisce delle piccole variazioni; invece,
in un termometro a colonnina di mercurio non si verificano scatti: la lunghezza della colonnina varia con
continuità, come la temperatura: una piccola oscillazione di
questa fa variare di poco la lunghezza della colonnina, mentre nel
termometro digitale o lascerebbe immutato il valore visualizzato o
lo farebbe aumentare di colpo di un grado;
allo stesso modo nel contagiri C2 l'indice sulla scala graduata cambia
posizione alla più piccola rotazione dell'oggetto di cui si
contano i giri, non solo al compimento di un giro completo, come fa
C1.
Questi, e più in generale i segnali che rappresentano un fenomeno che varia nel tempo
mediante un altro fenomeno che può variare con continuità
nel tempo, non solo a scatti, vengono detti segnali analogici.
La parola ricorda che si tratta di segnali che rappresentano il
fenomeno originale (la variazione della temperatura, la rotazione
dell'oggetto) mediante un fenomeno analogo (la variazione
della lunghezza della colonna di mercurio, lo spostamento
dell'indice). Le strumentazioni che usano rappresentazioni analogiche consentono una lettura precisa meno immediata ma consentono una rapida lettura approssimata e più efficaci valutazioni e confronti mentali (un tachimetro a lancetta consente di percepire visivamente la velocità a cui sto guidando con forme di stima meno laboriose di quelle che richiederebbe un visore digitale, un orologio a lancette consente di valutare meglio la collocazione delle ore nell'arco della giornata e dei minuti nell'arco dell'ora e di stimare rapidamente quanto tempo manca o è trascorso da un evento futuro o passato; …).
Alla voce
continuità sono rappresentati i grafici che corrispondono al contagiri analogico (C2) e quello digitale (C1) sopra raffigurati.
Il suono
Ritorniamo alla domanda iniziale. Come è possibile rappresentare un brano
musicale, che è un suono che varia con continuità,
mediante uno spartito musicale, che è di tipo digitale?
La musica è un suono particolare,
costituito da una successione di note, cioè piccoli
suoni dalle oscillazioni regolari. Consideriamo uno strumento musicale molto
semplice, costituito da una lamella metallica fissata per
un'estremità a un supporto (figura sotto a sinistra). Se spostiamo e rilasciamo
l'estremità libera della lamella, questa si mette a oscillare
con frequenza presso che costante, producendo un suono che,
trasformato in segnale elettrico, è rappresentabile
graficamente come segue (grafico a sinistra):
 |  |  |
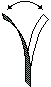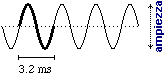In 3.2 ms questa particolare lamella compie un
ciclo, cioè compie una oscillazione completa,
che poi ripete immediatamente dopo allo stesso modo: 3.2 ms è il periodo; quindi
in 1 secondo (=1000 ms) la lamella compie 1000/3.2=310 (circa) cicli: il fenomeno si ripete con una frequenza
di 310 Hz. Ogni
1.6 ms il grafico attraversa la retta tratteggiata (una volta in "salita" e una volta in "discesa"); ciò
corrisponde ai passaggi della lamella per la "posizione di
riposo", cioè per la posizione in cui resterebbe se non
venisse sollecitata.
L'ampiezza
dell'intervallo costituito dai valori assunti dalla tensione (cioè, sul grafico, la variazione massima delle "y") dipende
dall'ampiezza dell'oscillazione della lamella; se, all'inizio,
avessimo spostato maggiormente la lamella dalla posizione di riposo,
avremmo ottenuto un grafico con ampiezza maggiore, ma non sarebbe cambiata la frequenza delle oscillazioni (questa
dipende solo dalle caratteristiche della lamella: materiale, lunghezza, spessore,
…).
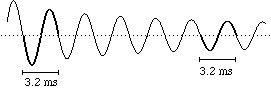
In
realtà, dopo la sollecitazione iniziale, l'ampiezza delle
oscillazioni della lamella man mano diminuisce, ma lentamente: il grafico
corrispondente (figura sopra a destra) non è altro che il grafico precedente deformato mediante una
progressiva riduzione della variazione verticale.
Dalla frequenza
del fenomeno, dipende la
altezza dell'effetto sonoro: maggiore è la
frequenza con cui vibra la lamella (ovvero, minore è il tempo
che impiega a compiere una oscillazione) più acuto
è il suono. Invece
dall'ampiezza dell'oscillazione dipende l'intensità
dell'effetto sonoro: maggiore è l'ampiezza, maggiore è
il volume del suono.
Per esempio se, suonando un'armonica a
bocca, soffio sempre nella stessa posizione ma con diversa intensità cambia il volume ma non l'altezza (è sempre la stessa lamella a vibrare); se invece cambio posizione muta anche l'altezza del suono: diventa più o meno acuto a seconda della direzione in cui mi sposto.
 | Nelle sirene le onde sonore sono prodotte soffiando aria contro un disco ruotante dotato di fori. Aumentando la velocità di rotazione viene prodotta un'onda sonora che oscilla sempre più velocemente, ossia un suono man mano più acuto. |
Un suono di altezza costante, che corrisponde a
un grafico periodico
o "periodico-smorzato", viene detto nota. Si estende anche al caso dello "smorzamento" il concetto di frequenza, anche se, a rigore, il fenomeno non si ripete
esattamente allo stesso modo.
Gli
strumenti musicali "meccanici" (a percussione, a fiato, …)
producono note con smorzamento. Solo con strumenti elettronici, in
cui le onde sonore sono prodotte da dispositivi alimentati
elettricamente, si possono produrre anche note non smorzate.
Una nota prodotta da uno strumento musicale, ad esempio una chitarra, corrisponde a un'onda che ha un grafico meno semplice di quello della lamella: una corda di una chitarra non ha una semplice oscillazione avanti e indietro come la lamella, ma vibra in modo più complesso; alla voce
periodo e frequenza è rappresentato il grafico corrispondente a una nota (un la dalla frequenza di 440 Hz) suonata da un particolare strumento. Se un medesimo
brano musicale viene eseguito al pianoforte o alla
chitarra, comprendiamo che si tratta dello stesso pezzo, anche se il
suono prodotto nei due casi è diverso: in corrispondenza della
stessa nota la corrispondente corda del piano e quella della chitarra
vibrano con la stessa frequenza, ma in modo diverso: ciascuno
strumento dà una sua "impronta" (o timbro)
alla nota; in altre parole si tratta di onde rappresentate da funzioni che hanno lo stesso periodo ma hanno grafici con forma anche molto diversa.
 | Un rumore è un suono che produce sensazioni sgradevoli. Il grafico corrispondente ha una forma "brutta", priva di regolarità. |
| Facciamo alcuni esperimenti con una specie di chitarra a una corda come quella raffigurata a lato, che possiamo costruire utilizzando una tavoletta di legno, due viti ad occhiello, una corda di nylon e una striscia di carta graduata. In alternativa possiamo usare una chitarra vera, e un nastro misuratore di lunghezze. |  |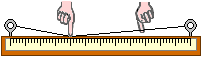
Se premiamo con un dito la corda in un punto qualsiasi e poi la pizzichiamo in un altro punto,
compreso tra il precedente e, ad esempio, l'occhiello destro, e ripetiamo più volte l'esperimento,
ci accorgiamo che, più il punto tenuto premuto è vicino all'occhiello destro, ossia più è
corto il tratto di corda che vibra, più è acuto il suono che viene prodotto.
Ciò non stupisce: la frequenza con cui oscilla una corda pizzicata,
come si può osservare facilmente a occhio nudo, è tanto più bassa quanto più lunga è
la corda.
Si può verificare che tale frequenza è inversamente proporzionale alla lunghezza della corda.
Facciamo un secondo esperimento.
Pizzichiamo la corda senza premere alcun punto e, poi, dopo aver premuto il punto di mezzo, e confrontiamo i suoni
prodotti. Ripetiamo l'esperimento generando e confrontando due altri suoni:
uno ottenuto premendo la corda in un punto qualunque e l'altro nel punto a metà tra il punto precedente
e l'occhiello.
Possiamo notare che ogni volta generiamo una coppia di suoni tra loro simili:
al dimezzarsi della lunghezza della corda vibrante, ovvero al raddoppiarsi della frequenza,
il nuovo suono è più acuto ma mantiene una somiglianza col precedente.
Il nostro orecchio è in grado di percepire se tra due suoni c'è questa somiglianza,
ossia se uno è ottenibile dall'altro mediante uno più raddoppi della frequenza.
Entrambi questi fenomeni sono stati scoperti sin dall'antichità, in quasi tutte le parti del mondo. Praticamente ovunque si è scelto un intervallo di suoni che va da una certa frequenza alla frequenza doppia e all'interno di esso si sono scelti in modo opportuni altri suoni. La serie di suoni così ottenuta è una cosiddetta scala musicale.
|
La scala musicale oggi utilizzata praticamente in tutto il mondo si basa sulle seguenti note "fondamentali", di cui abbiamo specificato le
frequenze (fra parentesi abbiamo indicato la
notazione anglosassone delle note, in genere usata anche dal software): DO (C) 261.6 Hz; RE (D) 293.7 Hz; MI (E) 329.6 Hz; FA (F) 349.2 Hz; SOL (G) 392.0 Hz; | |
Sono DO anche i suoni con frequenza (in Hz) 261.6/2, 261.6/4, 261.6/8, … e 261.6·2, 261.6·4, 261.6·8, … ; considerazioni analoghe valgono per le altre note. Ogni gruppo di note, da un DO al DO successivo (escluso), costituisce una ottava. Esistono anche altri tipi di "scale musicali", basati su note diverse. |  |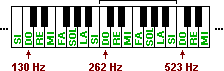
Qui puoi sentire riprodotta la scala delle note fondamentali. Il suono degli strumenti musicali oggi può essere, con buona approssimazione, prodotto con un computer. Qui trovi alcuni programmi che generano suoni simili a quelli di un pianoforte. Se vuoi, puoi esercitarti a "suonarli".
Nota. Le onde si distinguono in trasversali e in
longitudinali. Le onde trasversali sono quelle in cui i punti del mezzo perturbato si muovono
perpendicolarmente alla direzione di propagazione. Un esempio è costituito dall'onda su una corda:
i punti della corda si muovono in su e in giù.
Altro esempio sono le onde generate da un sasso che cade in uno stagno.
Sono onde che si possono propagare attraverso i mezzi solidi o sulla superficie dei liquidi.
Nelle onde longitudinali, invece, i punti del mezzo si muovono avanti e indietro parallelamente
alla direzione di propagazione. Questo è il caso del suono, discusso sopra, e di tutte le onde che si
possono propagare, oltre che attraverso i mezzi solidi, attraverso quelli liquidi e gassosi. Nel caso di un terremoto
dall'epicentro si propagano onde sismiche sia trasversali che longitudinali.
Nel caso della luce, delle onde radio e, più in generale, delle cosiddette onde elettromagnetiche
siamo di fronte ad onde longitudinali che non solo (come nel caso del suono) non trasportano materia,
ma non presentano neanche vibrazioni dell'aria o di un altro mezzo. In altre parole si tratta di fenomeni che non hanno una
natura "meccanica" e che possono propagarsi anche nel "vuoto". A queste conclusioni si è giunti solo alla
fine del XIX secolo. Le onde e i corpi materiali sono i due concetti fondamentali con i quali si può
descrivere il mondo fisico.
Un altro aspetto da richiamare relativo alle onde è che sia quelle luminose che quelle sonore possono essere tramesse
non solo per riflessione ma anche quando non c'è alcuna parete che le riflette
(si tratta del fenomeno della diffrazione, spiegato anch'esso alla fine del XIX secolo).
È da circa 4 mila anni prima di Cristo che gli uomini studiano le vibrazioni degli strumenti musicali. Ma è successivamente
allo studio di altri fenomeni periodici che si sono sviluppati gli attuali strumenti matematici con cui le si rappresentano. In particolare
fu decisivo lo studio delle oscillazioni degli oggetti sospesi mediante una corda. Fu Galileo, intorno al 1600, a
individuare la periodicità del moto di un pendolo che compie "piccole oscillazioni"; successivamente si svilupparono
gli orologi a pendolo. Vedi questo esercizio per approfondimenti.
La digitalizzazione dei suoni
Abbiamo visto nel punto precedente di questa voce che cosa sono le note e, quindi, compreso come un brano musicale può essere memorizzato mediante una opportuna sequenza di informazioni (che indicano le note da eseguire e la rispettiva durata di esecuzione), ad esempio mediante uno spartito o mediante un sequenza di istruzioni in un linguaggio di programmazione. Ciò non spiega come è possibile memorizzare l'esecuzione di un brano, cioè il suono prodotto da uno o più strumenti che lo eseguono: le note tengono conto solo della frequenza, non dei timbri, cioè delle forme d'onda delle note eseguite dagli specifici strumenti. In altre parole, come è possibile memorizzare in forma digitale le onde.
Incominciamo ad osservare che un
suono può essere riprodotto fedelmente non solo mediante
segnali elettrici, ma anche con altri fenomeni che varino con
continuità, cioè con altri tipi di segnali analogici.
Ad esempio può essere rappresentato su un nastro magnetico:
le variazioni nel tempo della tensione elettrica (che traducono le
vibrazioni della membrana del microfono) mediante un opportuno
dispositivo vengono trasformate in variazioni del livello di
magnetizzazione lungo il nastro che scorre.
In modo analogo vengono
registrati su un floppy-disk da un computer i segnali elettrici con cui, come abbiamo visto nel primo punto di questa voce, si possono
rappresentare le sequenze di bit.
In un CD, invece, si possono registrare "direttamente" i bit.
Sostanzialmente un CD è un disco che su sottilissime piste circolari concentriche presenta un'alternanza di tratti in rilievo e di zone piane. Per dare un'idea delle dimensioni, si pensi che i rilievi hanno altezza e larghezza dell'ordine di grandezza dei decimi di micron (1 micron - o micrométro - è pari a 10-6m). Le piste circolari vengono "lette" con un fascio laser (le zone piane vengono riconosciute sulla base del fatto che sono quelle che riflettono il fascio). Rilievi più lunghi vengono interpretati come 1; rilievi più corti come 0. |  |
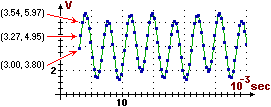
In modo un po' semplificato, possiamo dire che il segnale elettrico che traduce analogicamente un suono può essere "tabulato" (cioè descritto mediante una tabella di dati): ad esempio si può rilevare ogni tot tempo (nel caso della figura seguente ogni 0.27 millesimi di secondo) la tensione elettrica corrispondente e registrare la sequenza dei numeri che rappresentano queste misure. E ognuno di questi numeri può essere memorizzato con una codifica binaria.
|  |
Esistono delle tecniche e dei metodi matematici che, data la sequenza di numeri che corrisponde alla tabulazione di un segnale elettrico analogico, permettono di costruire automaticamente una "curva" che sia vicina al grafico originale. In questo modo è possibile ricostruire (a partire da queste informazioni digitali approssimate) suoni che siano il più possibile fedeli ai suoni originali. Vedi qui un esempio realizzato con R.
La digitalizzazione delle immagini
Qualcosa di analogo a quanto ora visto per il suono avviene per la digitalizzazione di una immagine. L'immagine viene scomposta in
tanti quadrettini; per ogni quadrettino si individua il colore
prevalente. Codificando i colori in forma binaria (ad es. il bianco con 0 e il nero con 1, nel caso del bianco-e-nero; o il bianco con 0000, il giallo con 0001, …, il nero con 1111 nel caso di una rappresentazione a 16 colori) possiamo
rappresentare l'immagine come la sequenza dei bit che codificano i
colori dei vari quadrettini. Se usiamo una griglia di 12·12 quadretti, il disegno in bianco-e-nero della
casetta sotto a sinistra può essere approssimato con la quadrettatura
raffigurata al suo fianco. A destra è rappresentato il
segnale digitale che codifica la quadrettatura. Più sotto è rappresentata un'altra immagine (un pezzo di girasole) e un suo ingrandimento.
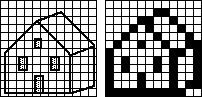 | 000000000000 000000110000 000011001000 000101000100 001000100010 010010010011 100000001101 101000101001 100000001101 100010001001 100010001011 111111111100 |
 | |
Sotto a sinistra sono raffigurati alcuni segmenti che si intersecano tracciati con l'applicazione Paint di Windows (o con un'altra applicazione
per realizzare immagini: PaintBrish, XPaint, MyPaint, …); a destra è raffigurato un ingrandimento dell'immagine. Le figure che appaiono come segmenti sono in realtà degli insiemi di quadretti: per
visualizzare immagini il calcolatore scandisce, in modo analogo all'esempio della "casetta", lo
schermo in quadretti (o rettangolini, in alcuni casi), detti
pixel, a ciascuno dei quali associa una sequenza di bit che ne rappresenta il colore.
Guardando l'immagine originale diremmo che ciascuna coppia di segmenti ha un punto in comune, ma, osservando l'ingrandimento, vediamo che nel caso della coppia centrale i segmenti non hanno neanche un pixel in comune e che in quello a destra ne hanno due, contraddicendo l'idea che due rette che si attraversino hanno uno e un solo punto in comune. In effetti ciò vale solo nella geometria astratta (e in particolare nella geometria piana euclidea), in cui i punti rappresentano posizioni esatte, e le rette hanno spessore nullo: il vantaggio di questa astrazione sta proprio nel "far finta" che le rette non parallele si intersechino esattamente in un punto, al di là del modo in cui le abbiamo disegnate, della loro disposizione, …: ciò facilita le descrizioni, i ragionamenti. Anche nel caso del tracciamento con una matita o con un gesso, i segmenti non si intersecherebbero esattamente in un punto, ma avrebbero in comune una zona dalla forma più o meno di parallelogramma: 
Nella voce calcolatore (5) sono approfonditi alcuni aspetti "software" della realizzazione delle immagini.
Qui
trovi qualche approfondimento su come sono realizzati e memorizzati i colori in un
documento software.
Esercizi: ,
