caso discreto.
Leggi di distribuzione (variabili continue)
Per una introduzione all'argomento rinviamo al primo paragrafo della analoga voce relativa al
caso discreto.
Funzioni di densità e variabili casuali continue
Per mettere a fuoco il tema partiamo con un esempio concreto:
| Una azienda produce pere Abate. La pere prodotte sono di varia misura (il peso va da poco più di un etto a quasi tre etti) e sono commercializzate sia "sfuse" che in confezioni "da 4 hg" composte da due pere. La legge richiede che una confezione venduta come "da 4 hg" contenga "almeno" 4 hg; quindi la azienda, per queste confezioni, seleziona pere con peso maggiore o uguale a 200 g e inferiore 210 g. Supponiamo che in questo intervallo le pere prodotte si distribuiscano uniformemente. |
Questa è una situazione "realistica", anche se (per facilitare le elaborazioni e mettere meglio in luce come avviene la modellizzazione) è stata inventata. Di fronte ad essa possiamo porci problemi come i seguenti:
(1) Qual è il peso medio di una confezione da "4 hg"?
(2) Qual è la probabilità che una di queste confezioni
ecceda il peso di 4 hg per meno di 8 g?
(3) E che lo ecceda per più di 12 g?
Modellizziamo la situazione utilizzando opportune variabili casuali.
Se indico con P1 il peso in decine di grammi di una pera e con P2
quello dell'altra, il peso (netto) in decine di grammi di una confezione posso rappresentarlo con P, avendo posto
So che P1 e P2 variano in
Il fenomeno è analogo a quello del lancio di 
due dadi equi: essi hanno uscite U1 e U2 distribuite uniformemente, la loro somma U no
(2 e 12 sono le uscite più improbabili, 7 è l'uscita più probabile).
Modellizzata la situazione possiamo studiarla sperimentalmente simulandola mediante il
generatore di numeri casuali.
Supponiamo di impiegare un linguaggio di programmazione in cui esso sia indicato con RND, possiamo simulare sia P1 che P2 con
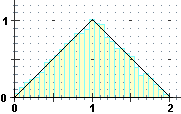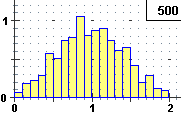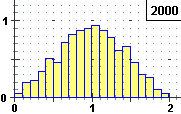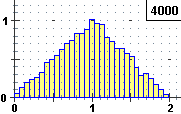
Si vede che l'istogramma delle frequenze relative tende a disporsi lungo un triangolo, analogamente
a quanto accadeva per i due dadi. Ma ora la variabile casuale P può assumere tutti i valori
di un intervallo, non un insieme di valori isolati come accadeva per U. La distribuzione teorica di P non potremo
rappresentarla con un istogramma, come nel caso della distribuzione di una variabile discreta.
|
Poniamoci, dunque, il problema di
come rappresentare graficamente la legge di distribuzione di una
variabile casuale continua. Partiamo dalla rappresentazione di una variabile continua X con distribuzione uniforme in |
 |
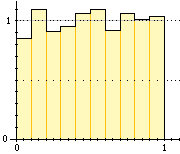Sopra a destra è illustrato un esempio di quello che si può ottenere con 1000 prove
suddividendo [0,1) in 10 intervallini. Come altezze delle colonne sono state prese le densità di frequenza,
ovvero le frequenze relative divise per l'ampiezza degli intervallini Distribuzione),
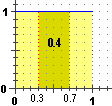
Il contorno superiore è il segmento con ordinata 1
e ascissa che varia tra 0 e 1. La probabilità che X cada tra 0.3 e 0.7 posso interpretarla (vedi figura sottostante a sinistra)
come l'area della figura che sta tra tale segmento, l'asse delle ascisse e le rette verticali di ascissa 0.3 e 0.7,
area che vale
 |
 |
 |
| X = RND | X = X1+X2, Xi = RND | P = P1+P2 |
Nel caso di X somma di due variabili continue uniformi, e in particolare X = X1+X2 con X1 e X2 distribuite uniformemente
in [0,1), che possiamo studiare con questa (o questa)
simulazione (X = RND+RND), otteniamo istogrammi
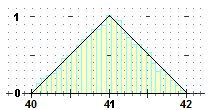
che tendono a disporsi lungo un contorno triangolare, proprio come abbiamo trovato per il caso delle pere abate
(P = 40+RND+RND):
sopra al centro quello che si ottiene per X, a destro quello che si ottiene per P.
|
Ora siamo in grado di affrontare i problemi posti all'inizio: • questione (2): la probabilità che il peso ecceda 40 decine di grammi per meno di 8 grammi è • analogamente, per la questione (3), abbiamo: • e il peso medio di una confezione? essendo il nostro triangolo simmetrico rispetto alla retta verticale di ascissa 41, 41 è anche l'ascissa del baricentro, e
lo assumiamo come media di P. |
 |
Consideriamo un'ulteriore situazione
problematica:
| L'organizzazione di vendite televisive Ventel riceve ordinazioni telefoniche tra le 14 e le 15. Per stabilire se il numero delle linee (e delle centraliniste) che impiega è conveniente fa studiare dalla ditta specializzata in statisiche Sifanstat i tempi di arrivo delle telefonate che arrivano ai centralini e le durate delle telefonate che riescono a prendere la linea. |
Negli istogrammi sotto raffigurati (relativi alle distanze temporali tra una telefonata e l'altra e
alle durate delle telefonate rilevate dalla Sifanstat ed espresse in secondi)
sull'asse verticale sono rappresentate le
densità di frequenza,
ossia le frequenze relative divise per l'ampiezza
dell'intervallo, in modo che l'area di ogni colonnina rappresenti la frequenza relativa con cui
un valore cade nell'intervallino di base, e che quella di ciascun istogramma sia complessivamente 1.
 |
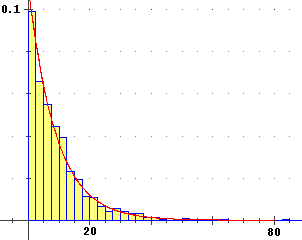tempi tra una telefonata e la successiva media = 8.97 w = 1/8.97 f(x) = w·e− w x |
 |
durate delle telefonate M = media = 49.3 S = s.q.m. = 19.2 | ||||||||||||
|
Il profilo superiore, se i rilevamenti sono molti, tende a disporsi per entrambi gli istrogrammi lungo due particolari curve,
descrivibili mediante le formule indicate a lato delle figure
(per e: funz. esponenziale e logaritmo). Curve di questo tipo la ditta SifanStat
le ritrova tutte le volte che esamina situazioni analoghe a quella che le ha chiesto di studiare la società Ventel.
Come si vede, si tratta di curve che sono il grafico di funzioni che dipendono solo dalla media (nel caso
dei tempi di attesa tra una telefonata e l'altra) o dalla media e dallo scarto quadratico medio (nel caso
delle durate delle telefonate).
Sono, ovviamente, solo modelli matematici che approssimano le situazioni reali: le ascisse del primo grafico variano
in [0,∞), quelle del secondo in
In entrambi i casi l'area tra grafico e asse orizzontale vale 1, come vedremo più avanti. Funzioni come queste, e come
quelle sul cui grafico si stabilizzavano gli istogrammi sperimentali di una distribuzione uniforme e della sommma di due distribuzioni unformi uguali,
si chiamano funzioni di densità.
|
Il nome deriva dal fatto che i valori di queste funzioni rappresentano le densità di frequenza teoriche: • se f è la funzione di densità corrispondente a una certa variabile casuale continua U, • quanto più I è piccolo tanto migliore è questa approssimazione; • in altre parole, se Δx è l'ampiezza di I, [ricorda:
(popolazione di R) = (densità popolazione)·(area di R)] |
 |
f funzione densità che rappresenta come si Pr(U ∈ I) ≈ |
Esercizio 1 (soluzione) Esercizio 2 (soluzione) Esercizio 3 (soluzione)
Media e scarto quadratico medio teorici
Il concetto di integrale
ci consente di approfondire e generalizzare quanto visto nei punti precedenti.
Se la variabile casuale U a valori nell'intervallo I ha istogrammi sperimentali che (all'aumentare delle prove e al ridurre l'ampiezza degli intervallini in cui viene ripartito I) hanno contorno superiore che tende a condondersi col grafico di una funzione f con dominio I, se f è integrabile su I posso porre, per ogni a e b in I:
Pr ( a ≤ U ≤ b ) =
Nota questa funzione, quindi, possiamo calcolare Pr(U∈J) per ogni intervallo J che sta nel dominio di U. f è dunque una caratterizzazione della legge di distribuzione di U. Come abbiamo anticipato nei paragrafi precedenti, f viene chiamata densità di probabilità [della legge di distribuzione] di U.
Ci occupiamo, nel seguito, di una variabile casuale U a valori in un intervallo di I per cui esista una funzione di densità f (non è detto che una tale f esista; quando parleremo di "variabile casuale continua" sottintenderemo che una tale f esista).
Sia f la densità di U. Posso definire la media M(U) di U in analogia al caso discreto:
|
se U fosse stata a valori in {v1, v2, v3, …} avremmo avuto
M(U) = ∫ I x·f(x) dx |  |
Per lo scarto quadratico medio abbiamo σ(U) = √Var(U), dove, posto
Var(U) = M(U - μ)2 =
[come per M(U) con al posto dei valori x di U i valori x-μ di U-μ]
Consideriamo le variabili casuali continue finora introdotte:
|
• Distribuzione uniforme in [0,1); densità: f(x) = 1. (vedi)
m = 0∫1 x·f(x) dx = 0∫1 x dx = [x2/2]x=1 − [x2/2]x=0 = 1/2 σ = √( 0∫1(x - m)2 f(x) dx ) = √( 0∫1(x - 1/2)2 dx ) =
|  |
| Con R potrei fare: f <- function(x) 1+x-x; g <- function(x) (x-1/2)^2*f(x) # metto 1+x-x invece che solo 1 in quanto il programma vuole la # comparsa della variabile di input integrate(g,0,1) 0.08333333 with absolute error < 9.3e-16 library(MASS); fractions(integrate(g,0,1)$value) [1] 1/12] |
|
Sperimentalmente (usando lo script a cui accedi da qui o usando i programmi R o Stat trovi (con almeno 1000 prove) media e s.q.m. molto vicini a 0.5 e 1/√12 = 0.2887. A destra è rappresentata sia la nostra funzione di densità che, più chiara, la funzione che ad x associa la probabilità che l'uscita sia minore di x, su cui ci soffermeremo tra quattro paragrafi.
|
• Distribuzione uniforme in [a,b): è la legge considerata sopra, con, rispetto ad essa, uscite moltiplicate per La densità è x → 1/(b-a), la media è (a+b)/2, lo s.q.m. è Nel caso in cui a = 0 e b = 1 ricado nel caso precedente, A lato è illustrato il caso della distribuzione uniforme in [0.4, 3.4]; la densità è x → 1/3; la media è 1.9 e lo s.q.m. è |
 |
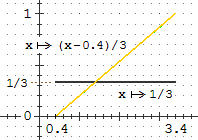• Distribuzione esponenziale; densità: f(x) = a e− a x, con a > 0 (è una delle due distribuzioni viste qui, per un a fissato)
m = 0∫∞ x·f(x) dx = 0∫∞ x ae-ax dx = 1/a 0∫-∞ueu du = 1/a (per i calcoli vedi questo esercizio)
σ = √( 0∫∞(x - 1/a)2 ae-ax dx ) = √(1/a2) = 1/a = m
Nel caso dell'esempio visto sopra la media m era il tempo medio tra una telefonata e la telefonata successiva. Hanno andamento simile le distribuzioni sperimentali dei tempi di attesa tra un arrivo e l'arrivo successivo di molti fenomeni (ad esempio della distanza temporale tra la venuta al semaforo di un'auto e la venuta dell'auto successiva, nel caso di semafori preceduti da un lungo tratto di strada senza altri impedimenti al traffico programmati dall'uomo; il parametro a, ossia il reciproco del tempo medio, in inglese viene chiamate rate, ossia "velocità").
[Con R potrei controllare il calcolo di media e s.q.m, o congetturarne sperimentalmente i
valori. Vedi quanto riportato sotto:
per w = 5 ∫[0,∞) g = 1 / w ;
∫[0,∞) h = (1 / w)2
f <- function(x) w*exp(-w*x); g <- function(x) x*f(x)
w <- 5
integrate(g,0,Inf)
0.2 with absolute error < 8.3e-05
# provo a visualizzare più cifre e a migliorare la precisione
print(integrate(g,0,Inf, abs.tol=1e-10), 10)
0.2 with absolute error < 2.9e-06
h <- function(x) (x-1/w)^2*f(x)
integrate(h,0,Inf)
0.04 with absolute error < 1.3e-05
# provo a visualizzare più cifre e a migliorare la precisione
print(integrate(h,0,Inf, abs.tol=1e-10), 10)
0.04 with absolute error < 6.8e-09 ]
Anche sperimentalmente si trovano media e s.q.m. molto vicini tra loro.
|
• Distribuzione gaussiana "di media 0 e scarto quadratico medio 1"; densità:
[Posso trovare che l'integrale di f e lo s.q.m. sono 1 con R: |
 |
Se considero la gaussiana "di media m", cioè
Se considero la densità gaussiana h "di s.q.m. σ", osservo che
• la distribuzione gaussiana "di media m e s.q.m. σ" ha effettivamente m e σ come media e s.q.m. (è la seconda delle due distribuzioni viste qui, per m e σ fissati):
| densità: f(x) = |
1 | e |
| |||||||
| ——— | ||||||||||
| √(2π) σ |
Nota 1. La funzione x → ∫ [−∞, x] h(t) dt
dove h è la gaussiana di s.q.m. σ è una funzione non elementare
[ intergrazione],
ossia il cui valore non può essere rappresentato mediante la composizione delle quattro operazioni, di
funzioni polinomiali, esponenziali, trigonometriche o loro inverse.
Soffermiamoci sulla distribuzione
gaussiana. Il suo nome deriva dal matematico (o fisico, naturalista, filosofo, …: le etichette
attuali avevano un significato diverso un paio di secoli fa) Gauss, che la studiò
particolarmente agli inizi dell'Ottocento; essa, in realtà, fu introdotta nel calcolo delle
probabiltà almeno una settantina d'anni prima; è nota anche come distribuzione
normale.
Il seguente script
o questo programma in R
(che utilizzano metodi di calcolo già accennati in punti precedenti)
consentono di calcolare direttamente integrali della "gaussiana". Vediamo un primo esempio d'uso di questa legge di distribuzione, sulla quale
torneremo più avanti, e di tale programma di calcolo.
La probabilità che un prodotto di un certo tipo sia difettoso è 1%. Qual è la probabilità che tra 10000 pezzi scelti a caso non ve ne siano più di 70 difettosi?
È un problema che dovrebbe essere risolto usando la legge di distribuzione binomiale,
che abbiamo già considerato studiando le
variabili casuali discrete:
Pr(N = k) = C(n,k) · pk · (1 – p)n-k.
Nel nostro caso dobbiamo calcolare Σk C(10000,k)·1%k·99%10000-k (k=0,…,70).
Usando R possiamo fare:
k <- seq(0,70,1); sum(choose(10000,k)*0.01^k*0.99^(10000-k))*100
ottenendo 0.092557: 0.09% è è la probabilità cercata.
Osserviamo tuttavia che il calcolo di C(10000,70)
eccede le capacità di molti degli usuali mezzo di calcolo (si verificherebbe un overflow);
basti pensare che (arrotondando)
Tuttavia nel nostro caso, come vedremo meglio in una voce successiva
limiti variabili casuali discrete],
Con lo script o i programmi precedenti calcolo l'integrale tra -0.5 e 70.5 della gaussiana; ho:
0.00151409587 se a = -0.5, b = 70.5, m = 100 e σ = 9.94987437 (= √99),
ossia:
0.15%.
Ho integrato tra questi estremi in quanto, passando dal finito al caso continuo,
i valori 0 e 70 corrispondono agli intervalli
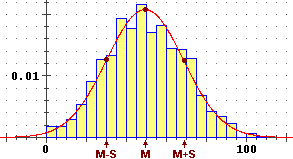
La media e lo scarto quadratico medio di una distribuzione
gaussiana permettono di determinare completamente la distribuzione: sono i due parametri che identificano la particolare densità gaussiana.
Nel caso della distribuzione esponenziale la densità è caratterizzata da un solo parametro: il valore della media, che coincide con quello dello scarto quadratico medio.
La legge di distribuzione uniforme in un intervallo di estremi a e b è, invece, completamente determinata dai valori di a e b −
Media e scarto quadratico medio danno delle indicazioni sulla forma e sulla posizione del grafico della funzione densità, ma, se non si conosce la forma di esso, e non si è in casi particolari come i precedenti, non sono sufficienti a determinarla. Possono essere di aiuto altri valori, di cui ne vediamo alcuni.
|
Nel caso in cui U sia una variabile casuale che
può assumere valori in un intervallo I di numeri reali, la mediana di U è definita come nel caso discreto
Se U è continua, viene chiamata moda di U ogni numero x di I per cui f(x) è massimo. Ovviamente − come nel caso discreto
|
 |
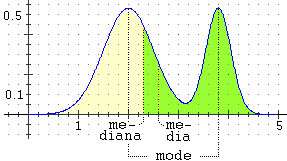Il confronto tra i diversi indici di posizione, mentre nel caso discreto può dare indicazioni sulla forma dell'istogramma di distribuzione, nel caso continuo può dare indicazioni sulla forma del grafico della funzione di densità. Le considerazioni geometriche svolte nel caso discreto valori
I seguenti grafici richiamano il significato geometrico
del "σ" di una gaussiana (o normale). Essi sono stati ottenuti con R
in cui la gaussiana (oltre che esplicitamente - vedi) può essere richiamata con il nome "dnorm" e i cui parametri (media e scarto
quadratico medio) sono indicati mean e sd (che sta per standard deviation, termine
che illustremermo in una voce successiva)
Si tratta dei grafici nel caso "media" = 0. Gli altri si ottengono con una semplice traslazione che porti l'asse verticale sulla ascissa di valore "media".
media <- 0 |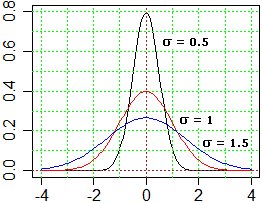 
|
L'andamento dei grafici per σ diversi conferma il fatto che σ è un indicatore della dispersione. Al diminuire di σ il grafico si innalza e si restringe. Come indicatore della "larghezza" del grafico potremmo assumere la ascissa del punto di flesso destro.
Il grafico della pendenza (realizzabile con R), sotto riprodotto solo per σ=1,
fa supporre che i punti di flesso (punti di estremo del grafico della pendenza) siano proprio in corrispondenza di
G <- function(x) dnorm(x, mean = media, sd = sigma)
media <- 0; sigma <- 1
plot(G,-4,4,ylim=c(-0.3,0.4)
abline(h=seq(-0.3,0.4,0.1),v=seq(-4,4,1),lty=3,col="green")
abline(h=0,v=0,col="brown",lty=3)
Gx <- expression( dnorm(x, mean = media, sd = sigma) )
Hx <-D(Gx,"x"); H <- function(x) eval(Hx)
plot(H,-4,4,add=TRUE,col="blue")
 |
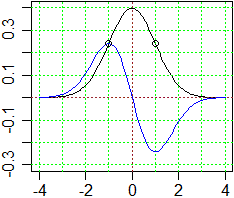Ciò può essere verificato calcolando e studiando la funzione derivata della densità gaussiana. Se calcoliamo l'area compresa tra grafico della densità gaussiana
(con m=0), asse x e rette |
Possiamo così precisare il senso in cui lo scarto quadratico medio, nel caso della densità gaussiana, è un indicatore della dispersione :
limiti
Esercizio 4 (soluz.) Esercizio 5 (soluz.) Esercizio 6 (soluz.) Esercizio 7 (soluz.) Esercizio 8 (soluz.)
Funzione di ripartizione
(o di distribuzione)
Sotto sono riprodotti sia il grafico della funzione di distribuzione uniforme in
quelli, analoghi, riferiti ad
un'altra distribuzione uniforme. In pratica, mentre il primo grafico corrisponde, sperimentalmente, all'istogramma
della distribuzione, il secondo corrisponde all'istogramma della frequenza cumulata, di abbiamo discusso
alla voce valori medi - 2 e di cui si
è vista la rappresentazione grafica in due approfondimenti (in questo e in quest'altro).
 |  |
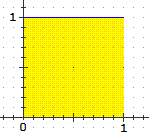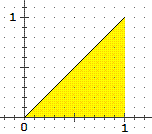| la funzione di densità (teorica) di RND: x → 1 | la sua funzione di ripartizione: x → Pr(uscita < x) = x |
Se U è una densità, viene detta ripartizione di U la funzione
Si noti che, nel caso in cui U sia continua, come nei casi visti sopra,
per ogni x (appartenente al dominio di U)
La contraddizione è solo apparente. Da una parte, la probabilità complessiva
non è data da una somma, ma, nel caso di U che vari con continuità in un intervallo,
da un integrale calcolo approssimato)
A volte si considera ripartizione di U è la funzione
• se t ≤ 1
Pr(X+Y < t) = (area del triangolo raffigurato divisa per l'area del quadrato) = |
|
Come ulteriore controllo possiamo tracciare il grafico della funzione densità
(dalla forma triangolare)
e quello della funzione di
Dal grafico di questa nuova funzione possiamo ritrovare che la mediana è 1, e, ad esempio, che la probabilità che l'uscita sia minore di 1.4 è, approssimativamente, 0.82 (col calcolo troviamo esattamente questo valore: −(x−2)2/2+1 per x=1.4 diventa −(1.4−2)2/2+1 = −0.36/2+1 = 0.82)
|
A destra come precedenti usando R. |
plot(c(-1,3),c(-1,2),type="n",xlab="", ylab="",asp=1)
abline(h=0,v=0,col="brown")
abline(h=seq(-1,2,0.5),v=seq(-1,3,0.5),lty=3,col="brown")
F <- function(x) 1-abs(x-1)
plot(F,0,2,add=TRUE)
n <- 1000; for(i in 0:n) {
a <- 0; b <- 2; x <- a+(b-a)/n*i
points(x,integrate(F,0,x)$value, pch=".", col="red") }
G <- function(x) x^2/2
plot(G,-1,3,n=100,type="p", col="red", pch=".", add=TRUE)
H <- function(x) -(x-2)^2/2+1
plot(H,-1,3,n=100,type="p", col="red", pch=".", add=TRUE)
# il grafico della retta y = x-1/2
abline(-1/2,1,lty=3,col="blue")
|
|
 |
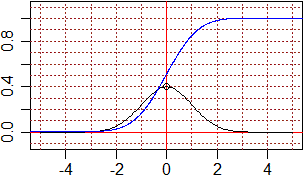G <- function(x) dnorm(x, mean = media, sd = sigma)
media <- 0; sigma <- 1
plot(c(-5,5),c(-0.1,1.1),type="n")
abline(h=seq(-0.1,1.1,0.1),v=seq(-5,5,1),lty=3,col="brown")
abline(v=0,h=0,col="red")
plot(G,-5,5,add=TRUE)
n <- 500; for(i in 0:n) {
a <- 0; b <- 5; x <- a+(b-a)/n*i
points(x,0.5+integrate(G,0,x)$value, pch=".", col="blue") }
n <- 500; for(i in 0:n) {
a <- 0; b <- -5; x <- a+(b-a)/n*i
points(x,0.5+integrate(G,0,x)$value, pch=".", col="blue") }
points(0,1/sqrt(2*pi))
Nota 2.
A differenza del caso finito,
non è detto che esista la media di una variabile aleatoria U (dotata di legge di distribuzione associata a una misura di probabilità Pr) nel caso continuo e nel caso discreto infinito.
Ad esempio la variabile U a valori in (1,∞) con densità f(x)=1/x2 (f è una densità in quanto 1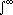
f =1) non ha media: l'integrale tra 1 e ∞ di 
x·f(x)
Analogamente se S è Σ 1/i2 (i da 1 a ∞) e Pr(U=i) = 1/(S·i2) (i intero positivo), la variabile aleatoria (a valori interi positivi) U non ha media.
Mentre nel caso discreto esiste sempre almeno
una moda, nel caso continuo non è detto che esista. Ad esempio se f(x)=1/(2√x), f è una funzione di densità tra 0 e 1 (ivi l'integrale è 1) che non ha massimo.
Esempio. Verificare che x → 1/(π·(1+x2)) è una funzione densità, determinarne la funzione di ripartizione, rappresentare graficamente le due funzioni (devi ottenere esiti come i seguenti).
[tale distribuzione, detta "di Cauchy", non ha media]
funzione densità
[ x → 1/(π·(1+x2)) ]
funzione ripartizione [ x → atn(x)/π+1/2 ]
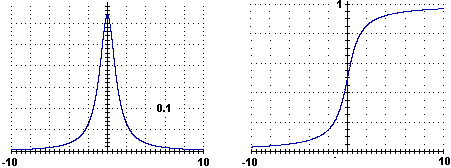
Nota 3. L'interpretazione geometrica della non esistenza della media della distribuzione di Cauchy a prima vista può lasciare perplessi: la figura delimitata dal grafico della funzione densità e dall'asse x, che ha area finita ed è simmetrica rispetto all'asse y, dovrebbe avere "baricentro" sull'asse y. Ma questa conclusione è frutto di un'ingannevole estensione al caso illimitato di una proprietà che varrebbe se la figura fosse limitata: se prendo un punto P sull'asse y non esistono i momenti rispetto a P delle due parti in cui la figura è divisa dall'asse y. Sotto, calcoli e grafici realizzati con R. Si noti che il programma dà, erroneamente, 0 come integrale della funzione di ripartizione tra −∞ e ∞ in quanto estende quanto accade tra −k ed k. Nel caso degli integrali tra −∞ e ∞ conviene sempre fare la somma dell'integrale da −∞ e 0 (o un qualunque numero k) e di quello tra 0 (o k) e ∞.
f <- function(x) 1/(pi*(1+x^2)) plot(f, -6, 6, ylim=c(-0.2,0.4)) abline(v=seq(-6,6,1),h=seq(-0.2,0.4,0.1),lty=3,col="red") abline(v=0,h=0,col="brown") g <- function(x) x*f(x) plot(g,-6,6,add=TRUE,col="blue") |
|
integrate(f,0,Inf)$value [1] 0.5 # e, per simmetria, tra -Inf e Inf vale 1 integrate(g,-10,10)$value [1] 0 integrate(g,-Inf,Inf)$value [1] 0 # valore (come osservato) non affidabile integrate(g,0,Inf)$value Errore in integrate(g, 0, Inf): maximum number of subdivisions reached # Faccio allora: integrate(g,0,1)$value [1] 0.1103178 integrate(g,1,100)$value [1] 1.355569 integrate(g,1e2,1e4)$value [1] 1.465855 integrate(g,1e4,1e6)$value [1] 1.465871 integrate(g,1e6,1e8)$value [1] 1.465871 # deduco che tra 0 e Inf è Inf |
|
Esercizio 9 (soluz.) Esercizio 10 (soluz.) Esercizio 11 (soluz.) Esercizio 12 (soluz.) Esercizio 13 (soluz.)
|
Nota 4.
La funzione di ripartizione può essere estesa anche al caso
discreto. Accenniamo alla cosa per informazione culturale, anche se, per il livello di approfondimento che
stiamo svolgendo, non sarebbe tecnicamente necessario. Consideriamo una variabile casuale U
che può assumere solo i valori 1, 2 e 3 e supponiamo che |
|
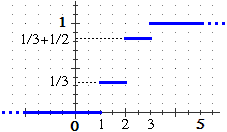
Vedi qui per un uso di R impiegando la libreria
