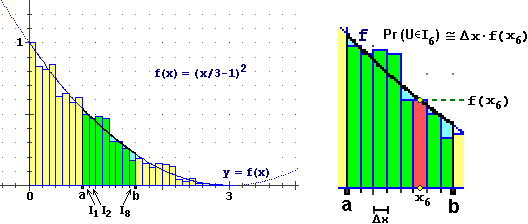L'integrazione [1ª parte] (2ª)
 L'integrazione studia, in generale, problemi di vario genere, da come • risalire al
grafico di una funzione
che rappresenta la posizione di un oggetto a partire da quello della sua velocità
a come • calcolare la probabiltà che una certa variabile casuale continua, di cui sia nota la distribuzione,
possa assumere valori compresi tra due numeri fissati, a come
• determinare il lavoro di una forza di cui sia noto come varia l'intensità al variare del punto di applicazione.
Esempi di questo tipo sono discussi nella parte
L'integrazione studia, in generale, problemi di vario genere, da come • risalire al
grafico di una funzione
che rappresenta la posizione di un oggetto a partire da quello della sua velocità
a come • calcolare la probabiltà che una certa variabile casuale continua, di cui sia nota la distribuzione,
possa assumere valori compresi tra due numeri fissati, a come
• determinare il lavoro di una forza di cui sia noto come varia l'intensità al variare del punto di applicazione.
Esempi di questo tipo sono discussi nella parte
 tre problemi introduttivi.
Quindi della definzione di integrale viene data una
tre problemi introduttivi.
Quindi della definzione di integrale viene data una  generalizzazione e sistemazione.
Segue un approfondimento dei legami tra integrazione e derivazione attraverso la messa a fuoco del
generalizzazione e sistemazione.
Segue un approfondimento dei legami tra integrazione e derivazione attraverso la messa a fuoco del
 teorema fondamentale del calcolo integrale.
Sono, infine, svolti alcuni
teorema fondamentale del calcolo integrale.
Sono, infine, svolti alcuni  approfondimenti e discusse alcune
approfondimenti e discusse alcune  difficoltà dell'integrazione, con riferimenti ad alcuni particolari insiemi di funzioni; questi
aspetti possono essere affrontati in un secondo tempo.
difficoltà dell'integrazione, con riferimenti ad alcuni particolari insiemi di funzioni; questi
aspetti possono essere affrontati in un secondo tempo.
Chi abbia già conoscenza dei concetti può saltare i "tre problemi introduttivi" e andare direttamente a
 generalizzazione e sistemazione.
generalizzazione e sistemazione.
 Tre problemi introduttivi
Tre problemi introduttivi
Primo problema (esistenza, e calcolo, dell'antiderivata)
v
= s'
(m/s)
|
 |
s
(m)
|
| t (s) |
|
Dal grafico della  velocità (in m/s) v in funzione del tempo (in s) t come posso risalire al grafico
della strada percorsa (in m) s in funzione di t ? velocità (in m/s) v in funzione del tempo (in s) t come posso risalire al grafico
della strada percorsa (in m) s in funzione di t ?
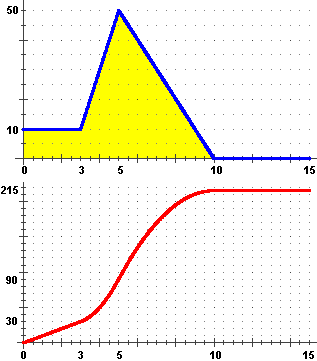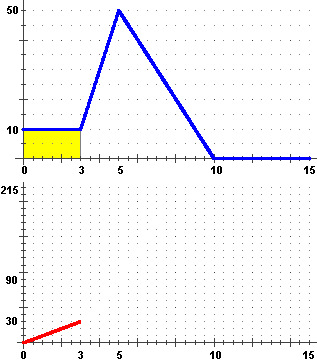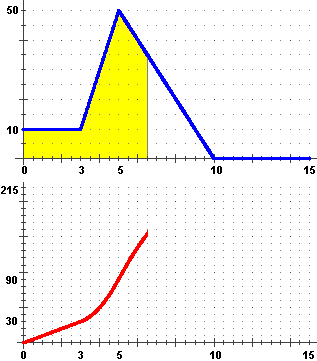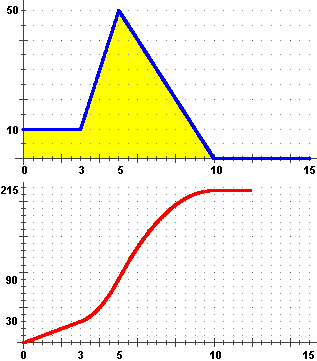
Intuisco che il grafico di s raffigurato a sinistra,
sotto a quello di v, sia corretto; v
non è altro che la derivata s' di s e il grafico di v
(quello sopra) sembra rappresentare come varia la pendenza lungo il grafico di s (quello sotto):
inizialmente questo ha pendenza costante (30/3 = 10), poi sale con la concavità verso l'alto,
ossia con pendenza via via crescente,
fino a t=5, in cui la pendenza inizia a diminuire, fino ad arrivare a t=10, in cui la pendenza diventa nulla.
Si intuisce pure che il grafico di s in funzione di t rappresenta anche
come varia l'area A delimitata (nel modo illustrato sotto a sinistra) dal grafico di v
(ovvero di s').
Sotto a destra puoi accedere ad una animazione che illustra meglio il fenomeno.
|
|
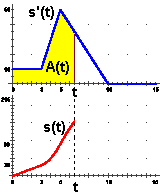 |
(vedi un'animazione con R) |
|
Qui puoi approfondire queste considerazioni. Dunque:
trovare il grafico di s in funzione di t a partire dal grafico di s'
in funzione di t
equivale a tracciare il grafico dell'area A(t) tra grafico di
s' e asse orizzontale che è compresa tra le rette verticali di ascissa 0 e di ascissa t.
|
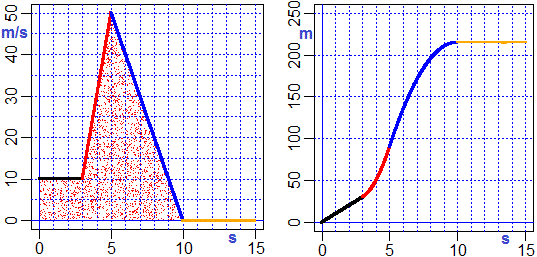
In realtà questa è una situazione ideale. Se non in casi particolari (come nel caso di un urto)
la velocità non può cambiare bruscamente.
Quanto visto per v vale per una qualunque funzione continua e positiva f:
una funzione g che abbia come derivata f (o, come si dice, che sia
una antiderivata di f)
è la funzione che ad x associa l'area A(x) delimitata dal grafico di f e l'asse orizzontale,
e compresa tra un input fissato
c e x.
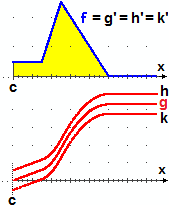
Naturalmente g non è l'unica funzione ad avere f come derivata. Qualunque funzione
che abbia come grafico quello di f traslato verticalemente ha la stessa derivata. Ad esempio se definisco
h(x) = g(x)+30 e k(x) = g(x)-30, ho D(h) = D(k) = D(g).
Nel caso dell'esempio iniziale, se con s indichiamo la posizione lungo la strada, oltre
alla s che ha grafico simile a quello di g, potremmo considerare s con grafico come quello di
h o di k, che corrisponderebbo a due altre situazioni in cui la posizione iniziale
è, rispettivamente, 30 m avanti o 30 m indietro, ma in cui al passare del tempo la velocità è
la stessa della prima situazione: si tratta di tre mezzi che avanzano mantenendo sempre la stessa distanza tra loro.
Un esempio di calcolo. |
 |
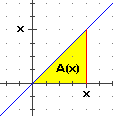 |
Cerco g che abbia f: x  x come derivata. x come derivata.
Prendo
g(x) = A(x) = "area tra grafico di f, asse degli input e rette verticali
di ascissa 0 e di ascissa x". Si tratta di un triangolo di base x e altezza x, quindi:
A(x) = x2/2.
Prendo dunque g(x) = x2/2. Verifica: g'(x) = Dx(x2/2) = 2x/2 = x : OK.
Avrei potuto prendere anche g(x) = x2/2+k con k costante qualunque.
|
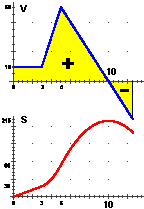
E se la velocità cambia segno?
Se, nel nostro esempio iniziale, arrivati a t=10, v invece che
mantenere il valore 0 continua a variare con lo stesso andamento diventando negativa (vedi grafico a destra in alto), ossia se il moto
inverte direzione, la posizione s arretra (vedi il grafico a destra in basso).
Per continuare a dire che l'area A(t) si comporta come s(t)
devo considerare negativo il contributo delle parti di superficie che stanno sotto all'asse degli input.
Questo equivale a considerare come area di ciascuno dei rettangolini considerati sopra il valore
v(t)Δt anche quando v(t) < 0.
 Notazioni
Notazioni
|
 |
Se f è una funzione continua nell'intervallo I = [a,b] si indica con
∫I f o con
∫[a, b] f, o nel modo indicato a lato,
l'area orientata della superficie compresa tra il grafico di f, l'asse orizzontale e le rette di ascissa a e di
ascissa b, dove con area orientata intendiamo indicare che si tratta del valore
ottenuto conteggiando come positivo/negativo il contributo delle parti di grafico con ordinata positiva/negativa.
Questo valore viene chiamato
integrale di f sull'intervallo I. |
|
| Il simbolo ∫ ha la forma di una "S" allungata.
Infatti ricorda che
l'area che sta sotto alla curva può essere approssimata sommando opportuni rettangolini. |
Se della funzione f si vuole indicare il termine generico occorre specificare
qual è la variabile che descrive la funzione. Ad esempio nel caso dell'esempio
precedente, f(x) = x, avremmo potuto scrivere:
A(x) = ∫0x f
oppure A(x) = ∫0x t dt
oppure A(u) = ∫0u x dx
oppure
A(x) = ∫0x f(t) dt
oppure
…
|
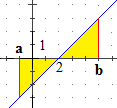
Nota. Abbiamo parlato di "area orientata" per poter cosiderare anche
le situazioni in cui il grafico sta sotto all'asse orizzontale. Il concetto di
 area,
invece, non dipende dal sistema di riferimento, e un'area non è mai negativa.
Ad esempio, nel caso della funzione f rappresenata a fianco, mentre possiamo dire che
∫[a,b] f = 0, ovvero che l'area orientata della figura
colorata è 0, dobbiamo dire che l'area della stessa figura è il doppio
dell'area di ciascun triangolino (e vale, quindi, 9). area,
invece, non dipende dal sistema di riferimento, e un'area non è mai negativa.
Ad esempio, nel caso della funzione f rappresenata a fianco, mentre possiamo dire che
∫[a,b] f = 0, ovvero che l'area orientata della figura
colorata è 0, dobbiamo dire che l'area della stessa figura è il doppio
dell'area di ciascun triangolino (e vale, quindi, 9).
|  |
 Secondo problema (le variabili casuali continue)
Secondo problema (le variabili casuali continue)
| Se l'istogramma della distribuzione statistica di una variabile casuale U è
approssimabile col grafico di una
funzione continua f per la quale so esprimere il termine f(x), |
| |
• come posso calcolare, utilizzando f, la probabilità che U cada in un intervallo [a,b]?
• come posso calcolare M(U)? |
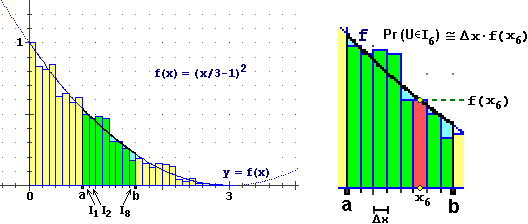
In questo caso il problema è in qualche modo rovesciato rispetto a quello
del paragrafo precedente:
dobbiamo trovare (per quanto riguarda il primo "•") l'area che sta tra il grafico di f,
l'asse orizzontale e le rette verticali di ascissa a e di ascissa b.
Nel caso rappresentato sopra
− f : x → (x/3−1)2 −
so trovare una g la cui derivata sia f e, quindi ( ), riconduco il calcolo dell'area cercata, ossia di ∫ [a, b] f ,
a quello di g(b) − g(a):
), riconduco il calcolo dell'area cercata, ossia di ∫ [a, b] f ,
a quello di g(b) − g(a):
D(g)(x) = (x/3−1)2
se
g(x) = (x/3−1)3 + k
dove k è una qualunque costante;
dunque
g(b) − g(a) = (b/3−1)3
−
(a/3−1)3
Nota. La f dell'esempio precedente, definita tra 0 e 3, è
effettivamente una funzione di densità:
non è negativa in [0, 3] e l'area tra il grafico e l'asse x vale 1:
∫ [0, 3] f = (3/3−1)3
−
(0/3−1)3
= 1.
Affrontiamo in modo simile il secondo "•".
| M(U) ≈ |
N | (xk· Pr(U ∈ Ik)) |
| Σ |
| k = 1 |
|
≈ |
|
e quindi, se U varia in I: |
M(U) = ∫ I x·f(x) dx
Nel caso della f dell'esempio precedente abbiamo che
la media è
∫03 x f(x) dx =
∫03 x(x/3−1)2 dx =
∫03 x(x2/9−2x/3+1) dx =
∫03 x3/9−2x2/3+x dx.
So trovare g(x) la cui derivata sia x3/9−2x2/3+x
e, quindi ( ), mi riconduco al calcolo di
g(3) − g(0): ), mi riconduco al calcolo di
g(3) − g(0):
g(x) = x4/36−2x3/9+x2/2+k;
media = 34/36−2·33/9+32/2
= 3/4. Generalizzando quanto visto per gli istogrammi ( figure 2), abbiamo che tale valor
medio corrisponde alla ascissa del baricentro della figura considerata,
a cui tendono gli istogrammi. figure 2), abbiamo che tale valor
medio corrisponde alla ascissa del baricentro della figura considerata,
a cui tendono gli istogrammi. | 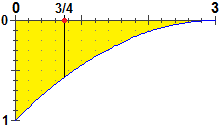 |
• E come posso trovare la mediana?
Nel caso discreto posso considerare l'istogramma della frequenza cumulata e trovare la
colonna più vicina al 50% (vedi)
In generale, se la variabile aleatoria è definita in un intervallo che ha
per estremo sinistro c, la mediana sarà il valore m
tale che
∫ cm f = 0.5.
Nel caso della f dell'esempio precedente, riferito a una variabile casuale definita
in [0, 3], abbiamo che
l'area che sta tra 0 e x è
(x/3−1)3 − (−1)3
che eguagliata a 50% dà luogo all'equazione:
(x/3−1)3 − (−1)3 = 1/2, la cui soluzione è la mediana:
(x/3−1)3 = 1/2 + (−1)3
(x/3−1)3 = −1/2
x = 3(1 − 1/21/3) =
0.61889842… | 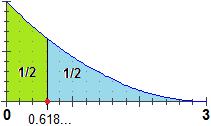 |
 Terzo problema (il lavoro di forze variabili)
Terzo problema (il lavoro di forze variabili)
Abbiamo visto ( proporzionalità inversa)
che il lavoro di una forza costante è dato dal prodotto
di questa per lo spostamento che ha generato nella sua stessa direzione,
come richiamato nel caso illustrato sotto a sinistra. proporzionalità inversa)
che il lavoro di una forza costante è dato dal prodotto
di questa per lo spostamento che ha generato nella sua stessa direzione,
come richiamato nel caso illustrato sotto a sinistra.
Il grafico a destra illustra la situazione nel caso particolare in cui la forza sia di 10 N, ossia
( vettori)
di circa 1.02 hg–forza:
il lavoro è proporzionale allo spostamento s eseguito, e varia come
l'area di un rettangolo di altezza fissata. vettori)
di circa 1.02 hg–forza:
il lavoro è proporzionale allo spostamento s eseguito, e varia come
l'area di un rettangolo di altezza fissata.
Che dire nel caso che
la forza cambi intensità, come nel caso ilustrato a destra, in cui
la forza esercitata via via aumenta?
| 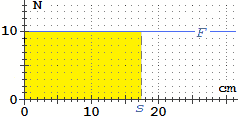 |
L = F · s |
|
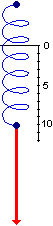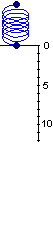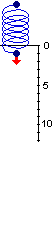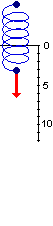 |
cm
? |
In questo caso particolare (legge di Hooke) sappiamo che la forza da esercitare sulla molla
per ottenerne un allungamento è
proporzionale all'allungamento stesso (almeno fino a
un certo valore di esso, dopo il quale la molla rimane deformata).
Quindi, se indichiamo con s l'allungamento della molla, abbiamo che la
forza da esercitare per ottenerlo è proporzionale al suo stesso valore (almeno fino
ad un certo valore), ossia
è del tipo
k · s dove k è una grandezza costante
fissata, che dipende dalle caratteristiche della molla.
Nel caso illustrato sopra, a destra, supponiamo che la molla si allunghi di
10 cm quando è sotto l'azione di una forza di 0.5 N.
A destra è illustrato il grafico di F in funzione di s, ossia di
F = 1/20 N/cm s.
È naturale prendere anche in questo caso come lavoro svolto
spostare della lunghezza s la molla l'area della figura delimitata
dal grafico di F e dall'asse orizzontale, fino alla retta verticale
corrispondente al valore di s:
il lavoro, in questo caso, cresce proporzionalmente sia ad s che a F (che
non è più costante).
Quest'area, come abbiamo già osservato nei precedenti esempi,
non è altro che l'integrale seguente, dove supponiamo che s sia espresso
in cm e che F sia espressa in N:
∫ [0, s] F
che, in base a quanto abbiamo visto, possiamo calcolare o usando il significato di area
o cercando un'antiderivata:
| 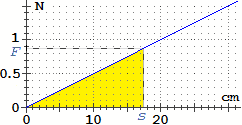 |
(area del triangolo) = F·s/2 = 1/20·s·s/2 = s2/40
(antiderivata rispetto ad x di 1/20·x) = 1/20·x2/2 = x2/40
la cui differenza per x tra 0 e s dà: s2/40
Quindi, usando le unità di misura, L = s2/40 J/cm2 (la divisione per
cm2 fa sì che il risultato sia J).
 Generalizzazione e sistemazione
Generalizzazione e sistemazione
• Che cos'è e come si calcola l'area. Alla voce
 area abbiamo visto come si
calcola quella dei rettangoli e dei triangoli, e, mediante la scomposizione in triangoli, quella di un
poligono qualunque. Abbiamo poi
area abbiamo visto come si
calcola quella dei rettangoli e dei triangoli, e, mediante la scomposizione in triangoli, quella di un
poligono qualunque. Abbiamo poi  visto diversi modi per determinare l'area di un cerchio. Le figure seguenti illustrano altri due
modi per trovare quest'ultimo valore, entrambi generalizzabili ad altre figure:
visto diversi modi per determinare l'area di un cerchio. Le figure seguenti illustrano altri due
modi per trovare quest'ultimo valore, entrambi generalizzabili ad altre figure:
 |
 |
| -1 | 1 |
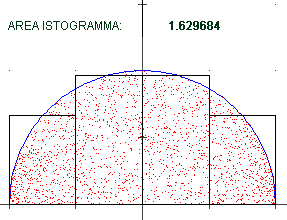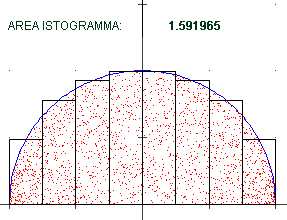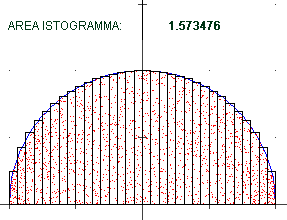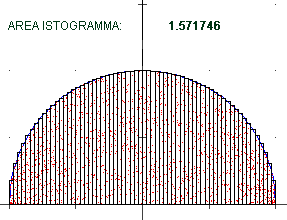
Il primo metodo consiste nell'approssimare una figura via via sempre meglio con un istogramma; l'area dell'istogramma
tende a stabilizzarsi su un certo valore che viene assunto come l'area della figura (nel caso illustrato si
tratta dell'area di un semicerchio di raggio uno, che vale
π / 2 = 1.570796326794896619231…). Vedi qui
per la semplice realizzazione di questo calcolo e queste immagini con R.
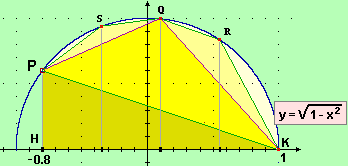
Il secondo metodo consiste nell'approssimare la figura con un trapezio dal numero dei lati crescenti (come trovare
facilmente l'area di un tale trapezio l'abbiamo visto alla voce  area): il valore su cui tende a stabilizzarsi coincide con quello ottenuto
col metodo precedente (vedi).
D'altronde (vedi figura a lato) l'equivalenza dei due procedimenti deriva dal fatto
che l'area di un trapezio è la somma di quella
di due opportuni rettangoli. area): il valore su cui tende a stabilizzarsi coincide con quello ottenuto
col metodo precedente (vedi).
D'altronde (vedi figura a lato) l'equivalenza dei due procedimenti deriva dal fatto
che l'area di un trapezio è la somma di quella
di due opportuni rettangoli. | 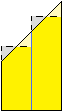 |
Tutti i metodi visti, nel caso dell'area di una figura che può essere interpretata come la parte del piano x,y che sta
tra il gafico di una funzione, l'asse x e due rette verticali x=a e x=b, si può dimostrare che
sono equivalenti al seguente metodo:
|
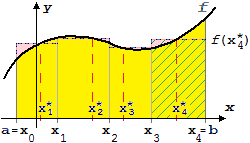 |
| |
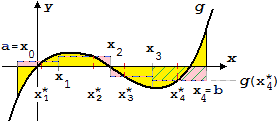
si suddivide l'intervallo [a, b] in N intervallini,
si sceglie a caso un numero
x i* nell'i-mo
intervallino (i che va da 1 a N),
si fa la somma delle aree dei rettangoli che hanno per base tali intervallini e per altezza il valore che
la
funzione assume nel numero scelto; se tale valore, al tendere a 0 dell'ampiezza massima degli intervallini,
tende a stabilizzarsi su un unico numero A, allora A viene assunto come area della figura considerata.
|
Come  osservato, per ricordare
che il calcolo è effettuato mediante una somma, l'area è indicata con una S un po' allungata:
A = ∫ [a, b] f,
oppure con ∫ [a, b] f(x) dx
(se vuoi puoi pensare intuitivamente il termine come la somma infinita di
tanti rettangolini di base infinitesima dx e di altezza f(x) al variare di x tra a e b).
I numeri a e b sono i valori tra cui viene considerata f. osservato, per ricordare
che il calcolo è effettuato mediante una somma, l'area è indicata con una S un po' allungata:
A = ∫ [a, b] f,
oppure con ∫ [a, b] f(x) dx
(se vuoi puoi pensare intuitivamente il termine come la somma infinita di
tanti rettangolini di base infinitesima dx e di altezza f(x) al variare di x tra a e b).
I numeri a e b sono i valori tra cui viene considerata f. |
Sopra è illustrato il caso N = 4 ed è evidenziato il quarto rettangolino dell'unione di rettangoli che approssima l'area A della figura
rappresentata. L'area dell'intera unione è:
(x1−x0) · f(x1*)
+ (x2−x1) · f(x2*)
+ (x3−x2) · f(x3*)
+ (x4−x3) · f(x4*)
Se come figura consideriamo quella tra il grafico di f e una retta orizzontale di ordinata k (ossia il
grafico della funzione x → k), come nel caso raffigurato sotto a sinistra, possiamo togliere
all'area di f considerata nel modo precedente l'area del rettangolo punteggiato sotto al centro,
ossia considerare l'area raffigurata per ultima.
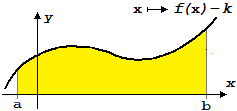
È evidente che l'area che sta sotto al grafico della funzione costante k è quella di un
rettangolo: ∫ [a, b] k dx = (b−a)k
e che l'area che sta sotto alla funzione x → f(x)−k è pari alla differenza
tra ∫ [a, b] f(x) dx
e ∫ [a, b] k dx. In formule:
∫ [a, b] f(x) dx
=
∫ [a, b] f(x) − k dx
+
∫ [a, b] k dx
e
∫ [a, b] f(x) − k dx =
∫ [a, b] f(x) dx −
∫ [a, b] k dx
|
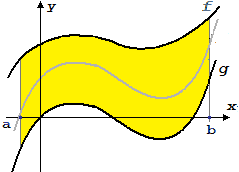
Analogamente, a una figura come quella a destra associamo l'area data da:
|
 |
|
∫ [a, b] f(x) dx
−
∫ [a, b] g(x) dx
|
| È naturale estendere il procedimento al caso raffigurato sotto, in cui g
ha il grafico che contiene tratti sottostanti all'asse x:
nel valutare
∫ [a, b] g(x) dx
basta considerare negativi i contributi dei rettangoli rivolti in basso (sotto, a destra,
è raffigurata l'approssimazione della figura delimitata dal grafico di g e dall'asse x
per una particolare suddivisione dell'intervallo dato in quattro parti).
|
 |
∫ab g(x) dx |
 |
Il procedimento descritto inizialmente  si estende quindi naturalmente anche al caso in cui il grafico di f abbia tratti
sottostanti all'asse x, a patto di considerare negativi i contributi dei rettangoli
rivolti in basso, e di chiamare integrale
invece che area il valore ottenuto:
si estende quindi naturalmente anche al caso in cui il grafico di f abbia tratti
sottostanti all'asse x, a patto di considerare negativi i contributi dei rettangoli
rivolti in basso, e di chiamare integrale
invece che area il valore ottenuto:
si fa la somma dei prodotti
(xi − xi-1)
· f(xi*)
- che sono positivi o negativi a seconda del segno di f(xi*) -
e se tale valore, al tendere a 0 dell'ampiezza massima degli intervallini,
tende a stabilizzarsi su un certo numero I, I viene assunto come integrale di f
tra a e b, e viene indicato con il simbolo
a ∫ b f.
L'uso del simbolo della S allungata e del termine "integrale" è frutto di un accordo raggiunto verso la fine del 1600
dai matematici (e fisici, filosofi, …) Leibniz e Newton.
 Sembra facile, pensando al significato di area, dimostrare che tutte le funzioni continue in un intervallo [a, b]
sono ivi integrabili, ossia che se f è una di esse si può trovare un unico numero I tale che
I = ∫[a, b] f,
ma non lo è affatto.
Noi prendiamo questo per buono (lasciando a chi è interessato una traccia della
Sembra facile, pensando al significato di area, dimostrare che tutte le funzioni continue in un intervallo [a, b]
sono ivi integrabili, ossia che se f è una di esse si può trovare un unico numero I tale che
I = ∫[a, b] f,
ma non lo è affatto.
Noi prendiamo questo per buono (lasciando a chi è interessato una traccia della
 dimostrazione) e, più in generale, prendiamo per buona la seguente proprietà
:
dimostrazione) e, più in generale, prendiamo per buona la seguente proprietà
:
se f è una funzione continua in [a, b] o è ivi limitata e discontinua in al più un
numero finito di punti, allora esiste ∫[a, b] f
Questo risultato ci autorizza a scegliere nel modo più comodo la suddivisione dell'intervallo [a, b],
dato che si può dimostrare che (nel caso in cui la funzione soddisfi le ipotesi citate) in ogni caso il
processo al limite converge verso il valore cercato.
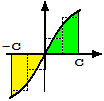 |
In particolare, nel caso la funzione sia (inoltre) dispari
( funzione-2)
abbiamo che ∫[−c, c] f = 0
qualunque sia il numero c positivo che scegliamo:
basta prendere rettangoli uguali e diversamente orientati (in su e in giù),
simmetricamente rispetto all'origine, in modo che la somma con segno delle aree si annulli.
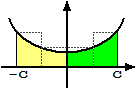
Nel caso, invece, che la funzione sia (inoltre) pari i rettangoli, presi in modo analogo, hanno arre che si sommano,
per cui ∫[−c, c] f = 2 ∫[0, c] f funzione-2)
abbiamo che ∫[−c, c] f = 0
qualunque sia il numero c positivo che scegliamo:
basta prendere rettangoli uguali e diversamente orientati (in su e in giù),
simmetricamente rispetto all'origine, in modo che la somma con segno delle aree si annulli.
Nel caso, invece, che la funzione sia (inoltre) pari i rettangoli, presi in modo analogo, hanno arre che si sommano,
per cui ∫[−c, c] f = 2 ∫[0, c] f
|  |
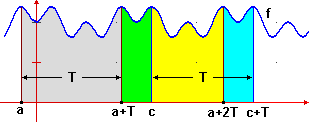
Nel caso di funzione f che (inoltre) sia periodica
( periodo e frequenza)
abbiamo che se T è il periodo ed I e J sono due intervalli ampi T, allora ∫ I f =
∫ J f.
La figura a lato illustra l'equaglianza di
∫[a, a+T] f,
∫[c, c+T] f
e di
∫[a+T, a+2T] f.
Per la dimostrazione basta prendere opportunamente rettangolini uguali nei diversi intervalli di ampiezza T. periodo e frequenza)
abbiamo che se T è il periodo ed I e J sono due intervalli ampi T, allora ∫ I f =
∫ J f.
La figura a lato illustra l'equaglianza di
∫[a, a+T] f,
∫[c, c+T] f
e di
∫[a+T, a+2T] f.
Per la dimostrazione basta prendere opportunamente rettangolini uguali nei diversi intervalli di ampiezza T.
Nel caso sottostante al precedente è illustrato un caso specifico: la funzione che
ad x associa x − int(x) (ad x si sottrae la sua parte intera).
È una funzione non continua che tra −1 e 2 ha come integrale 3·0.5 = 1.5.
Pensando al significato di integrale come area è facile capire (e non sarebbe difficile dimostrare,
ragionando sui rettangolini, come abbiamo fatto sopra) che se f e g sono integrabili su [a, b]
allora ∫[a, b] f + g =
∫[a, b] f +
∫[a, b] g e
∫[a, b] f − g =
∫[a, b] f −
∫[a, b] g.
Altrettanto facile è dimostrare che se k è un numero qualunque
∫[a, b] k f =
k ∫[a, b] f (basti pensare
a un cambio di unità di misura sull'asse verticale).
| 
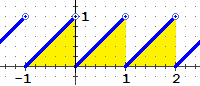 |
Esempio 1
∫ [−2, 2] x3 + 2 dx =
∫ [−2, 2] x3 dx +
∫ [−2, 2] 2 dx =
(in quanto x → x3 è dispari)
0 + 4·2 = 8
|  |
Esempio 2
∫ [−2, 2] (x3 + 2)/8 dx =
1/8 ∫ [−2, 2] x3 + 2 dx =
... =
1/8 · 8 = 1
|
 |
Un'altra convenzione comoda è quella di ammettere integrali in cui gli estremi di intergrazione siano il
primo maggiore del secondo, e, più precisamente, di porre
∫[b, a] f = − ∫[a, b] f.
In altre parole, si valutano in modo opposto, oltre le parti di area con l'ordinata negativa rispetto a quelle con
l'ordinata positiva (come già abbiamo fatto sopra  ),
anche le parti di area con l'ascissa che viene percorsa
in verso opposto. Nel caso della funzione f raffigurata a fianco, per esempio, possiamo scrivere: ),
anche le parti di area con l'ascissa che viene percorsa
in verso opposto. Nel caso della funzione f raffigurata a fianco, per esempio, possiamo scrivere:
∫ [2, 5] f = 4.5, ∫ [5, 2] f = −4.5,
∫ [−1, 3] f = ∫ [−1, 2] f + ∫ [2, 3] f =
−4.5 + 0.5 = −4,
∫ [3, −1] f = −∫ [−1, 3] f = 4.
|
Inoltre, se f è integrabile tra a e b,
tra b e c, e tra a e c
∫ [a, b] f +
∫ [b, c] f =
∫ [a, c] f
Esempio
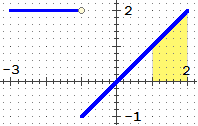
g : x → 2 se x > −1, g : x → x altrimenti
∫ [−3, 2] g = ∫ [−3, −1] g +
∫ [−1, 1] g + ∫ [1, 2] g =
∫ [−3, −1] 2 dx +
0 + ∫ [1, 2] x dx =
2·2 + 0 + 3/2 = 11/2
|  |
Nota.
Nell'esempio precedente abbiamo calcolato ∫ [−3, −1] g
come se g(x) valesse 2 in tutto l'intervallo [−3, −1],
non solo in [−3, −1).
Questo è lecito in quanto l'area di un segmento (come l'integrale tra −1 e −1 stesso
di una qualunque funzione) è nulla. Questa osservazione sta, più in generale, dietro alla possibilità
di scrivere, anche quando f non è continua in b:
∫ [a, b] f +
∫ [b, c] f.
 Formula fondamentale del calcolo integrale
Formula fondamentale del calcolo integrale
In molte situazioni non è affatto facile trovare direttamente l'integrale di una funzione continua. In queste
situazioni può essere di aiuto quanto già, informalmente, osservato all'inizio  , che possiamo precisare nel seguente modo:
, che possiamo precisare nel seguente modo:
sia f continua in [a, b]; se G' = f allora
∫ [a, b] f = G(b) − G(a)
Quest'ultima espressione viene spesso chiamata formula fondamentale del calcolo integrale in quanto consente di
ricondurre il calcolo di un integrale definito di f alla ricerca di una sua primitiva, ossia di una funzione che abbia
f come derivata, semplificando notevolmente il lavoro in molti casi. Anch'essa fu scoperta e dimostrata, più o meno
contemporanemente e indipendentemente, verso la fine del XVII secolo,  dal tedesco Leibniz e dall'inglese Newton.
Facciamo alcuni esempi, per confermare la
validità della formula, evitando di darne una dimostrazione più rigorosa della spiegazione fatta
dal tedesco Leibniz e dall'inglese Newton.
Facciamo alcuni esempi, per confermare la
validità della formula, evitando di darne una dimostrazione più rigorosa della spiegazione fatta
 nell'esempio iniziale.
nell'esempio iniziale.
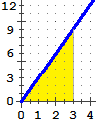
• f: x → 3x; ∫ [0, t] f = ?
come G tale che G' = f posso prendere G: x → 1.5x2;
quindi
∫ [0, t] f = ∫ [0, t] 3x dx =
G(t) - G(0) =
1.5t2 − 1.5·02 = 1.5t2.
Verifichiamo la cosa col significato di integrale:
l'area che sta tra il grafico di f, l'asse x e le rette x = 0 e x = t
è l'area di un triangolo di base t e altezza 3t, ossia è t·3t/2 = 1.5t2: OK.
|
|
• ∫ [−2, 2] x3 + 2 dx = ?
Dx (x4/4 + 2x) = x3 + 2;
∫ [−2, 2] x3 + 2 dx =
[x4/4 + 2x]x=2
−
[x4/4 + 2x]x=−2
=
(16/4+4) − (16/4−4) = 8 − 0 = 8.
Ritroviamo in questo modo quanto trovato sopra
 usando direttamente la definizione di integrale (anche se, questa volta, in modo più complicato).
usando direttamente la definizione di integrale (anche se, questa volta, in modo più complicato).
|
• ∫ [1, 3] 1/t dt = ?
Dx log(x) = 1/x
( funzioni esponenziale e logaritmo);
∫ [1, 3] 1/t dt =
[log(x)]x=3 − [log(x)]x=1 =
log(3) − log(1) =
log(3).
funzioni esponenziale e logaritmo);
∫ [1, 3] 1/t dt =
[log(x)]x=3 − [log(x)]x=1 =
log(3) − log(1) =
log(3).
In questo caso non sarebbe stato facile trovare tale eguaglianza usando direttamente la definizione di integrale.
Il fatto che valgano le proprietà  che permettono di ricondurre l'integrale di una somma di funzioni e della moltiplicazione per una costante di una funzione
agli integrali delle singole funzioni, analoghe alle proprietà già viste per le
che permettono di ricondurre l'integrale di una somma di funzioni e della moltiplicazione per una costante di una funzione
agli integrali delle singole funzioni, analoghe alle proprietà già viste per le
 derivate,
è un'ulteriore conferma del legame tra integrazione e derivazione.
derivate,
è un'ulteriore conferma del legame tra integrazione e derivazione.
L'integrazione (2ª parte)
 Approfondimenti
Approfondimenti
A causa del legame tra derivazione e integrazione (espresso dal teorema fondamentale) si è presto diffuso l'uso di
∫ f(x) dx per indicare un generico termine
g(x) tale che g'(x) = f(x);
l'operazione che ad f(x) associa tale termine viene chiamata (oltre che antiderivazione) integrazione indefinita,
mentre l'aggettivo definita viene riservato all'associazione alla funzione e ad un intervallo
[a, b] del numero ∫ [a, b] f.
È un uso che sopravvive per motivi storici, ma che è abbastanza ambiguo, e usato in modi differenti.
Per chi lo affronta per la prima volta è bene, dunque, fare alcune osservazioni:
• nel caso dell'integrale definito la variabile "integrata" è
muta : si potrebbe
scrivere ∫ [-1, 3] f(x) dx
o ∫ [-1, 3] f(t) dt
o ∫ [-1, 3] f,
o usare una variabile diversa da x e t
in modo del tutto equivalente;
invece ∫ f(t) dt, ∫ f(x) dx e ∫ f(u) du
indicano termini diversi;
• qualcuno usa l'integrale indefinito per indicare un insieme di termini:
∫ f(x) dx = {g(x) + c / c numero reale}:
ad es. ∫ 6x dx starebbe per l'insieme costituito dai termini
3x2,
3x2 + 1,
3x2 + 2/3,
3x2 − 5, …,
ovvero dai termini del tipo
3x2 + c al variare di c in IR,
altri (come noi faremo) un termine particolare che abbia come derivata f(x);
• noi useremo quest'ultima convenzione, ogni tanto esplicitando, e ogni tanto no,
la possibilità di aggiungere una costante, ossia qualche volta scriveremo ∫ 6x dx = 3x2
e qualche altra volta ∫ 6x dx = 3x2 + c
lasciando al lettore la comprensione; il software, più rigorosamente, usa solo la prima convenzione; ad esempio Maple
fornisce i seguenti risultati, lasciando all'utente la possibilità di aggiungere una costante qualunque:
∫ 6x dx = 3x2
∫ x − 1 dx =
x2/2 − x
∫ t3 + 2 dt =
t4/4 + 2t
Le prime due colonne della tabella seguente, e i primi quattro elementi delle terza,
riassumono alcune derivate e alcuni integrali d'uso comune, che
è bene pian piano incominciare a memorizzare. Gli elementi successivi delle terza colonna possono essere consultati
all'occorrenza; è, comunque, un buon esercizio verificare che le derivate
di essi sono gli elementi della prima.
| ∫ g(x) dx |
g(x) |
|
| f(x) |
f '(x) |
∫ f(x) dx |
k
xn
1/x
ex
log(x)
ax (a > 0, a ≠ 1)
loga(x) (a > 0, a ≠ 1)
sin(x)
cos(x)
tan(x)
asin(x)
acos(x)
atan(x)
|
0
n xn−1
−x−2
ex
1/x
ax log(a)
1 / x / log(a)
cos(x)
−sin(x)
cos(x)−2 [=
1+tan(x)²]
1 / √(1−x2)
−1 / √(1−x2)
1 / (1+x2)
|
kx
xn+1/(n+1) (se n ≠ −1)
log(x) , log(−x)
ex
x log(x) − x
ax / log(a)
(x log(x) − x) / log(a)
−cos(x)
sin(x)
−log(cos(x)) , −log(−cos(x))
x asin(x) + √(1−x2)
x acos(x) − √(1−x2)
x atan(x) − log(1+x2)/2
|
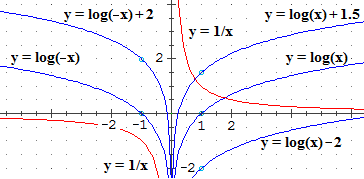
Si noti che come integrale di 1/x si sono messe due espressioni: log(x) e log(-x).
È da intendersi che la funzione che ad x positivo associa log(x) + h
e che a x negativo associa log(−x) + k, dove h e k sono
numeri reali qualunque, ha come derivata 1/x.
Infatti per x>0 d (log(x)+h) / dx
=
d log(x) / dx+
d h / dx
= 1/x e per x<0 d (log(−x)+k) / dx
=
d log(−x) / dx+
d k / dx
= −1/x·( −1) = 1/x.
Considerazione analoghe valgono per altre funzioni: nella tabella è descritto il caso di tan(x).
Esercizio.
Trovare
∫
(ex + x−2 +
x + 3) dx.
Cerco f tale che
df / dx =
ex + x−2 + x + 3.
|
 |
Basta che f sia la somma delle funzioni che in x hanno come derivate
ex, x−2, x e 3.
dex / dx = ex,
d − x−1 / dx =
x−2,
d (x2/2) / dx = x,
d 3x / dx = 3 dx / dx = 3·1 = 3.
Quindi va bene f(x) = ex − x−1 + x2/2 + 3x
e, più in generale, f(x) = ex − x−1 + x2/2 + 3x + c al variare di c in IR.
|
 Difficoltà dell'integrazione
Difficoltà dell'integrazione
Se derivo o integro una funzione polinomiale ottengo ancora una funzione polinomiale.
Ad es. se F(x) = 3x2+x−3√2 ho che
F'(x) = 6x+1 e che ∫ F(x) dx =
x3+x2/2−3√2x+c,
al variare di c in R.
Consideriamo le cosiddette funzioni razionali, ossia esprimibili cone rapporto tra due funzioni polinomiali. La derivata
di una di esse è ancora una funzione razionale, come conseguenza immediata delle regola per la derivazione del rapporto di due funzioni.
Ma l'integrazione di una funzione razionale non è detto che sia tale. Ad esempio l'integrale rispetto ad x di 1/x è log(x), o log(−x), che non sono
razionali.
[In qualche libro di testo le funzioni razionali che sono rapporto tra due funzioni polinomiali di primo grado vengono chiamate
(a sproposito, e, a questo livello, in modo non comprensibile) funzioni omografiche.
Il termine corretto è trasformazione lineare fratta (linear fractional transformation, in sigla LFT). Le omografie si occupano di
questioni più generali, che qui non possiamo trattare]
Di fronte a una funzione espressa mediante una formula usuale siamo sempre in grado di esprimerne mediante
una formula la derivata e l'integrale? Dobbiamo precisare che cosa intendiamo per "formula usuale":
se chiamiamo funzioni elementari le funzioni ottenibili mediante successive composizioni di funzioni polinomiali,
di elevamento a potenza, esponenziali, logaritmiche, circolari e circolari inverse, la risposta è positiva per la derivazione
(abbiamo visto tutti i procedimenti per derivare una funzione elementare ottenendo una funzione elementare), ma è
negativa per l'integrazione.
Ad es. so che
d (1/√(x4+1) / dx = −2x3/√((x4+1)3); infatti
la composizione di x → u = x4+1, u → y = u−1/2
ha come derivata dy/dx = dy/du·du/dx =
−1/2u−3/2·4x3 = −2x3/√(u3).
Ma non si riesce a trovare un termine descritto mediante le usuali funzioni che sia uguale a
∫ (1/√(1+x4) dx.
Un altro esempio: di fronte a F(x) = ex2
- che sta per e^(x^2) -
so che F'(x) = 2x ex2
ma non riesco a trovare alcuna funzione elementare la cui derivata sia F(x).
Qualche altro esempio di funzioni, espresse con x come variabile di input, che sono nelle stesse condizioni:
√(x3+1),
sin(x2),
cos(ex),
sin(x)/x,
ex/x,
1/log(x). In effetti solo una piccola minoranza delle funzioni elementari ha antiderivata elementare. Vedi come calcolarne gli
integrali qui.
Nota. In altre parole, le funzioni elementari non sono altro che le F tali che F(x) può essere espresso con
un termine in cui appaiono, applicati direttamente o indirettamente a x, solo i simboli log, exp, sin, cos, tan,
arcsin, ..., oltre a quelli di somma, prodotto ed elevamento a potenza (e quelli di divisione e di estrazione di radice, che sono un
caso particolare di elevamento a potenza).
Un esempio di funzione non elementare che studierai è la funzione di ripartizione della gaussiana.
Un altro esempio è la funzione n → n! (che è non elementare in quanto coinvolge una quantità
di operazioni che cresce con n).
Esercizio (e soluzione)
Si parla anche di funzioni
algebriche per indicare quelle ottenibili
componendo funzioni razionali ed estrazioni di radici (non solo quadrate), e, più in generale, ogni funzione
che sia esprimibile come soluzione di una equazione polinomiale (come la funzione F dell'esempio seguente).
Ad esempio y = (x - 1)2/3+ k, che equivale a y = 3√((x - 1)2) + k, esprime y come funzione algebrica di x, mentre y = sin(kx2) no, in
quanto compare la funzione seno applicata a kx2. Un esempio più complesso è la funzione F tale che
F(x)5+F(x)4+x = 0, che non è esplicitabile in forma elementare.
Esercizio (e soluzione)
Si parla anche di funzioni
trascendenti per indicare le funzioni non algebriche.
Sono tali, ad esempio, le funzioni trigonometriche e le esponenziali.
Il software di calcolo simbolico ogni tanto esprime gli integrali usando simboli di funzione
come sinh e cosh. Queste funzioni sono chiamate rispettivamente
seno iperbolico e coseno iperbolico in quanto, in modo abbastanza simile alle
funzioni seno e coseno, hanno la caratteristica che D(sinh) = cosh e D(cosh)= sinh. Inoltre,
così come la curva x=cos(t), y=sin(t) al variare di t è un cerchio, così
la curva x=cosh(t), y=sinh(t) al variare di t è un ramo di iperbole avente le bisettrici
dei quadranti come asintoti.
Si ha che sinh(x) = (exp(x)-exp(-x))/2 e che cosh(x) = (exp(x)+exp(-x))/2.
Per qualche approfondimento vedi qui.
Su alcune particolari tecniche che possono essere utili
per calcolare alcuni integrali si tornerà alla voce  calcolo di integrali.
calcolo di integrali.
I metodi di calcolo approssimato degli integrali definiti discussi
 sopra,
generalizzati e migliorati, sono presenti in molte applicazioni di tipo matematico.
Qui trovi come usare R per effettuare questi calcoli.
Qui trovi più in generale come si può usare R
per integrare le funzioni.
sopra,
generalizzati e migliorati, sono presenti in molte applicazioni di tipo matematico.
Qui trovi come usare R per effettuare questi calcoli.
Qui trovi più in generale come si può usare R
per integrare le funzioni.
 Numeri
trascendenti
Numeri
trascendenti
Gli aggettivi trascendente e algebrico sono usati, in matematica, anche con altri significati, che val
la pena di richiamare:
si dice (circa dal 1750) trascendente un numero (reale o complesso) che non è soluzione di alcuna
equazione polinomiale a coefficienti interi; si dice algebrico un numero (reale o complesso) che non è
trascendente, ovvero che è soluzione di qualche equazione polinomiale a coefficienti interi.
Si può provare che π e che e, oltre ad essere irrazionali,
sono trascendenti. Le dimostrazioni sono recenti, rispettivamente
del 1882 e del 1873. Tuttora vi sono molti numeri che si sanno esprimere mediante gli
usuali simboli funzionali e che non si sa se siano trascendenti o no (ve ne sono anche che non
si sa neanche se siano irrazionali o no: vedi).
Per citare
due esempi, ricordiamo che si è dimostrato solo, rispettivamente, nel 1979 e nel 2003
che 2√2 e che π/atan(1/2) sono
trascendenti.
Osserviamo, per finire, che la terminologia con cui vengono classificati i numeri e le
funzioni ha un'origine storica, legata a un periodo in cui le conoscenze e gli usi della matematica era
molto limitati rispetto agli attuali, e non deve essere confusa con i significati che "elementare",
"trascendente", … hanno in altri ambiti. Ricordiamo, per esempio, i numeri non trascendenti ora richiamati e la funzione fattoriale,
considerata in uno degli esercizi precedenti, che non è
una funzione elementare.
Esercizi: 


 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 L'integrazione studia, in generale, problemi di vario genere, da come • risalire al
grafico di una funzione
che rappresenta la posizione di un oggetto a partire da quello della sua velocità
a come • calcolare la probabiltà che una certa variabile casuale continua, di cui sia nota la distribuzione,
possa assumere valori compresi tra due numeri fissati, a come
• determinare il lavoro di una forza di cui sia noto come varia l'intensità al variare del punto di applicazione.
Esempi di questo tipo sono discussi nella parte
L'integrazione studia, in generale, problemi di vario genere, da come • risalire al
grafico di una funzione
che rappresenta la posizione di un oggetto a partire da quello della sua velocità
a come • calcolare la probabiltà che una certa variabile casuale continua, di cui sia nota la distribuzione,
possa assumere valori compresi tra due numeri fissati, a come
• determinare il lavoro di una forza di cui sia noto come varia l'intensità al variare del punto di applicazione.
Esempi di questo tipo sono discussi nella parte
 tre
tre generalizzazione
generalizzazione teorema
teorema approfondimenti
approfondimenti difficoltà
difficoltà generalizzazione
generalizzazione





 x come derivata.
x come derivata.