Le funzioni esponenziale e logaritmo [1ª parte] (2ª)

  La crescita esponenziale

Supponiamo che sia possibile organizzare l'allevamento di una certa specie di animali in modo tale che ogni anno il numero dei capi aumenti circa della metà, cioè venga moltiplicato per 1.5. Vogliamo studiare come aumenterebbe il numero dei capi al passare del tempo, escludendo che vengano venduti o eliminati capi.     Se indichiamo con P(n) il numero per cui si è moltiplicata la popolazione iniziale dopo n anni, ossia se P(n) è la popolazione misurata prendendo come unità la popolazione iniziale, possiamo descrivere la situazione così:   P(0) = 1, P(n+1) = P(n) · 1.5.   Quindi: P(1) = 1·1.5 = 1.5,  P(2) = 1.5·1.5 = 2.25,  P(3) = 2.25·1.5 = 3.375,  ... P(8) = 17.08…·1.5 = 25.62…,  ... P(20) = 2216.8…·1.5 = 3325.2…,  ... : ad es. dopo 20 anni la popolazione arriverebbe ad essere più di 3000 volte quella iniziale.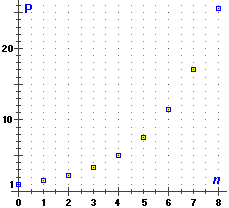

    Sia dal calcolo dei valori che dal grafico a destra, che rappresenta P in funzione di n, si vede che all'aumentare di n P(n) cresce in maniera esplosiva.  Si dice che P(n) ha una crescita esponenziale, in quanto, come è facile capire pensando alla definizione di potenza, P(n) può essere espresso come:
  P(n) = 1.5ⁿ   (ossia mediante il calcolo di una potenza che ha l'input come esponente).
    Poiché ad ogni anno la popolazione cresce di una quantità pari al 50% della popolazione dell'anno precedente, la velocità con cui la popolazione varia annualmente è proporzionale alla popolazione stessa.  Possiamo interpretare la cosa anche sul grafico, calcolando la pendenza dei segmenti che si otterrebbero congiungendone i punti:
il primo segmento, che congiunge i punti (0,P(0)) e (1,P(1)), ha pendenza:
ΔP / Δn = (P(1)-P(0))/(1-0) = (1.5-1)/1 = 0.5.   Il secondo:
ΔP / Δn = (P(2)-P(1))/(2-1) = (P(1)·1.5-P(1))/1 = P(1)·0.5.   In generale:
ΔP / Δn = (P(n+1)-P(n))/1 = (P(n)·1.5-P(n)) = P(n)·0.5.
    In altre parole, la pendenza dei vari tratti rettilinei secondo cui si sviluppa il grafico cresce proporzionalmente alle ordinate.

Esercizio (e soluzione)

  Una situazione analoga è quella della crescita di un deposito in una banca. Per evidenziare l'analogia con l'esempio precedente supponiamo che la banca applichi un interesse del 50% annuo (nella realtà le banche applicano tassi estremamente più piccoli, per cui non si osserva la crescita "esplosiva" che invece evidenzia il grafico seguente). Supponiamo che il deposito iniziale sia di 100 € e che non vengano nel frattempo fatti altri versamenti (e non vengano fatti prelevamenti). Se esprimiamo il tempo t in anni, il deposito in euro D(t) dopo t anni è descrivibile come:
  D(0) = 100,  D(t+1) = D(t) · (1 + 50/100) = D(t) · 1.5   ovvero:
  D(t) = 100 · 1.5^t

    Mentre sopra aveva senso valutare la popolazione dell'allevamento solo di anno in anno, qui ha senso considerare anche tempi t non interi: una persona può ritirare i soldi anche in momenti diversi dalla fine dell'anno, ad esempio dopo 5.5 anni.
    Il calcolo del valore del deposito in questi casi non viene fatto usando la formula, ad esempio calcolando 100·1.5^5.5, ma si calcolano i valori del deposito dopo 5 e 6 anni con 100·1.5⁵ e 100·1.5⁶ e si calcolano quelli intermedi facendo variare il deposito proporzionalmente al tempo.
    In altre parole, invece del grafico di t 100 · 1.5^t come quello punteggiato sotto a destra, si considera quello che si ottiene da esso congiungendo i punti ad ascissa intera con dei segmenti:

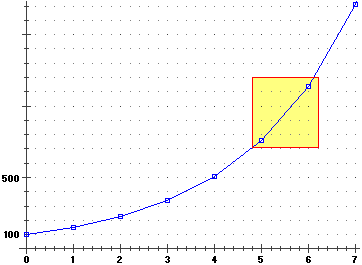
    Facendo i conti: 100·1.5⁵ = 759.38, 100·1.5⁶ = 1139.06; dopo 5 anni e mezzo: 759.38 + (1139.06-759.38)/2 = 949.22. Mediante l'uso diretto della formula invece si sarebbe ottenuto:  100·1.5^5.5 = 930.04.

    Questo è dunque un caso in cui l'andamento è "esponenziale" restringendo il dominio a input t interi, ed è "lineare" in ciascun intervallo tra un input intero e il successivo.

    Un altro esempio di fenomeno a crescita esponenziale è stato discusso alla voce velocità di variazione. Fenomeni a crescita esponenziale si incontrano anche nello studio dei problemi combinatori: vedi il seguente esercizio:

Esercizio (e soluzione)

  L'esempio iniziale dell'allevamento era poco realistico, ma facile per introdurre l'argomento. Vi sono situazioni in cui le popolazioni hanno effettivamente un andamento esponenziale. È il caso di vari tipi di microrganismi unicellulari che si riproducono per scissione:  quando la cellula raggiunge una certa dimensione si scinde in due. In particolari condizioni ambientali all'interno di una popolazione di una di queste specie di microrganismi il tempo medio di vita di una cellula (ossia il tempo medio che passa dalla scissione di una cellula a quello di una cellula da essa generata) è pressocché costante. In alcuni microrganismi esso può essere di pochi minuti, in altri può essere di qualche giorno.
    In queste condizioni esiste un intervallo di tempo T (tempo di duplicazione) tale che, passando da un qualunque istante t all'istante t+T, la popolazione raddoppi:  infatti gli organismi non si scindono tutti esattamente nello stesso tempo, cosicché nel complesso di una popolazione di svariati milioni di individui si ha un ininterrotto duplicarsi di cellule che dà luogo a una crescita della popolazione praticamente continua e regolare, con velocità di variazione proporzionale alla popolazione stessa.

    Se iniziamo a misurare la popolazione a partire da un certo istante t=0 e indichiamo con P(t) il numero per cui si è moltiplicata dopo il tempo t, ossia se P(t) è la popolazione misurata prendendo come unità la popolazione iniziale, possiamo descrivere la situazione così:
        P(0) = 1,   P(t+T) = P(t)·2

ovvero P(t) = 2ⁿ  se n è il numero delle duplicazioni avvenute nel tempo t.
Tenendo conto che n lo si ottiene dividendo t per il tempo di duplicazione T, abbiamo anche:
        P(t) = 2 ^{t / T}.

    In questo caso la formula è praticamente applicabile per ogni t, per cui, se da un rilevamento sperimentale ogni 5 minuti otteniamo i valori di P rappresentati graficamente sotto a sinistra, ha senso cercare di approssimare tali punti con una curva, come è fatto sotto a destra.

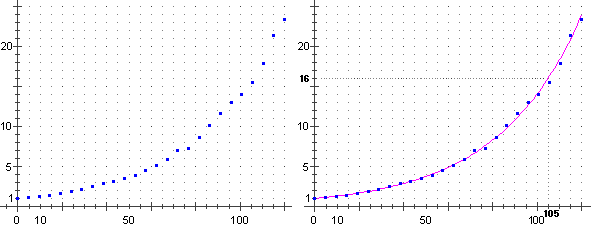
    Ricaviamo che la popolazione si moltiplica per 16 in 105 minuti; 16 = 2⁴; quindi 4T = 105 minuti. Questi microrganismi duplicano la loro popolazione in 105/4 = 26.25 minuti, ossia in 26'15".

    L'andamento di P in questo caso è dunque descrivibile con la funzione t 2 ^{t / 26.25}. Poiché [] 2 ^{t / 26.25} = (2^1/26.25)^t e 2^1/26.25 = 1.0268, possiamo descrivere il fenomeno anche con la formula:
        P(t) = 1.0268 ^t.

    Nel punto successivo vedremo come calcolare la velocità di variazione all'istante t di fenomeni descritti mediante funzioni del tipo t a ^t.

  Le funzioni esponenziali e la loro derivazione

Negli esempi precedenti abbiamo visto che le funzioni esponenziali, ossia del tipo  F: x a ^x con la base a positiva (se no non potrebbero essere definite su tutto R) e diversa da 1 (se no si tratterebbe della funzione costante x 1), esprimono fenomeni in cui una grandezza F(x) cambia con una velocità di variazione proporzionale a F(x) stessa.  Ci aspettiamo, quindi, che la derivata F'(x) sia del tipo k·F(x).  Verifichiamo la cosa ricorrendo alla definizione di derivata:

lim h→0  ax+h – ax ———— h

=

lim h→0 ax  ah – 1 ——— h

=

ax  lim h→0  ah – 1 ——— h

=

ax  ( d ax )x=0 —— d x

Dunque ho proprio che D_x(a^x) = k·a^x dove k è la derivata in 0.

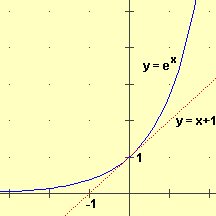	Tra tutte le funzioni esponenziali, ha una particolare importanza quella per cui tale k (cioè la derivata in 0) è 1, ossia che ha come derivata sé stessa.  Il valore della base per cui ciò accade viene indicato con e, numero che viene chiamato numero di Nepero. La animazione a cui si accede cliccando qui dà un'idea di come si può determinare e, e trovare che:   e = 2.71828182845904… (si tratta di un numero irrazionale).
	Dunque x e x è la funzione esponenziale il cui grafico nel punto (0,1) ha pendenza 1.     y = ax con a > e ha tangente in (0,1) con pendenza maggiore di 1; se 1 < a < e la pendenza è positiva e minore di 1; se 0 < a < 1 la pendenza è negativa.     y = hx e y = (1/h)x, in quanto h–x = 1/(hx) = (1/h)x, hanno grafici tra loro simmetrici rispetto all'asse y [ funzione(2)].	x ax

Dunque  D_x(e^x) = e^x.
    Questa particolare funzione esponenziale, usatissima in matematica e nelle sue applicazioni, viene spesso scritta "a 1 piano" usando il simbolo exp, ossia scrivendo exp(x) al posto di e^x.

    Le derivate delle altre funzioni esponenziali possono essere ricondotte a questa. Vediamolo ad es. nel caso di x 2^x:
• cerco di esprime 2 come e^... ; la cosa è fattibile ricorrendo al grafico di x 2^x e a qualche procedimento per tentativi; ad es. usando una calcolatrice a 8 cifre posso trovare che 2.7182818^0.69314718 = 2; quindi, approssimando a 8 cifre, 2 = e^{0.69314718…}
• 2^x posso dunque scriverlo approssimativamente come (e^0.69314718)^x e quindi [] come e^{0.69314718·x}
• il grafico di x 2^x = e^{0.69314718·x} è quello di x e^x [] scalato orizzontalmente dividendo le ascisse per 0.69314718; la pendenza dunque viene moltiplicata per 0.69314718;

• in definitiva, Dx(2x) = k·2x dove k è il numero tale che ek = 2.     In modo del tutto analogo ho che, se a > 0, Dx(ax) = k·ax dove k è il numero tale che ek = a.     In pratica, se indichiamo con il simbolo log la funzione inversa di x ex, possiamo scrivere che k = log(a), ovvero che:  Dx(ax) = log(a)·ax. Nel caso particolare in cui a = e ritroviamo la formula Dx(ex) = ex in quanto log(e) = 1: il numero a cui elevare e per ottenere e è 1.     Le funzioni inverse delle funzioni esponenziali si chiamano funzioni logaritmiche. Di esse si occupa il prossimo punto.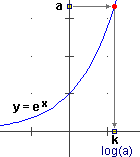

Esercizio (e soluzione)

Le funzioni esponenziale e logaritmo (2ª parte)

  I logaritmi

Quando diciamo che l'ordine di grandezza [ rappresentazione decimale dei numeri] di 1000 è 3 o che quello di 96 mila è 4, e quasi 5, intendiamo dire nel primo caso che si tratta di 10³, nel secondo caso di un numero compreso tra 10⁴ e 10⁵, e molto vicino a 10⁵.
    Il concetto di ordine di grandezza facilita la descrizione sia dei valori molto grandi (milioni, miliardi, …) che di quelli molto piccoli (milionesimi, miliardesimi) e, come vedremo, la loro rappresentazione grafica. Consideriamo, ad esempio, il diagramma seguente e la sua didascalia.

L'orecchio di una persona di udito buono rileva solo i suoni con frequenza compresa tra, circa, 20 Hz e 20000 Hz ( calcolatore 4): il timpano non è in grado di vibrare a una frequenza che stia fuori da questo intervallo e, quindi, l'orecchio non può trasformare un suono con una frequenza di questo tipo in impulsi nervosi da inviare al cervello. I grafici a lato riportano, per due categorie di persone, come al variare della frequenza (in Hz) dei suoni cambia il volume minimo (in dB, decibel: unità di misura per l'intensità, o volume, del suono) a cui si riesce a percepirli. I suoni meglio percepiti sono quelli attorno ai 3000 Hz.

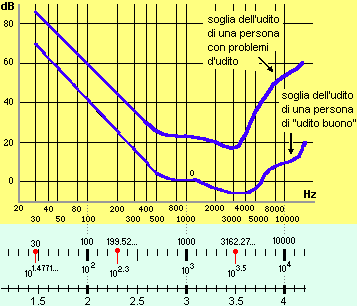Per visualizzare meglio l'andamento è stata scelta una scala orizzontale "sproporzionata" realizzata nel modo raffigurato a destra:

i valori delle frequenze sono stati segnati in corrispondenza dei loro ordini di grandezza rappresentati su una usuale scala proporzionata; ad es. 100 sulla scala dei grafici corrisponde alla tacca 2 degli ordini di grandezza in quanto 10²=100, 1000 corrisponde alla tacca 3 in quanto 10³=1000; 30 è stato segnato in corrispondenza di 1.4771… in quanto 10^1.4771…=30.

    Nel fare ciò abbiamo esteso il concetto di ordine di grandezza passando dalle potenze ad esponente intero a quelle ad esponente reale. Potremmo dire che l'ordine di grandezza di 30 è 1.4771…, ma, come sappiamo, si preferisce dire che è 1. Si dice, invece, che 1.4771… è il logaritmo decimale di 30; simbolicamente si scrive: 1.4771… = Log(30). In pratica il logaritmo decimale è un'estensione del concetto di ordine di grandezza.
    In modo sintetico possiamo dire che la funzione Log è la funzione inversa di x 10^x:
h è il logaritmo decimale di k se 10^h = k.

    La scala per le frequenze usata nel diagramma precedente viene chiamata scala logaritmica in quanto i valori sono rappresentati a distanze proporzionali non ai valori stessi ma ai loro logaritmi decimali. Si tratta di una scala che si usa quando si vogliono rappresentare assieme valori con ordini di grandezza molto diversi: in una usuale scala come avremmo potuto rappresentare assieme 30, 50, 80 e 5000? non saremmo stati in grado di differenziare i primi tre valori, che si sarebbero ammucchiati in uno stesso punto dell'asse.

Esercizio (e soluzione)

  Nei punti precedenti abbiamo introdotto due esempi di funzioni logaritmiche, ossia di funzioni inverse di funzioni esponenziali:
• la funzione log, inversa di x e^x, detta logaritmo naturale e indicata anche col simbolo ln,
• la funzione Log, inversa di x 10^x, detta logaritmo decimale.
    Più in generale per ogni numero positivo a diverso da 1, si chiama logaritmo in base a e si indica log_a, la funzione inversa di x a^x. In particolare abbiamo che  Log = log₁₀ e che  log = log_e.
    Ecco i grafici di due funzioni logaritmiche, una con base maggiore di 1, l'altra con base minore di 1, con tratteggiati i grafici delle funzioni esponenziali di cui sono le inverse:

Esercizio (e soluzione)

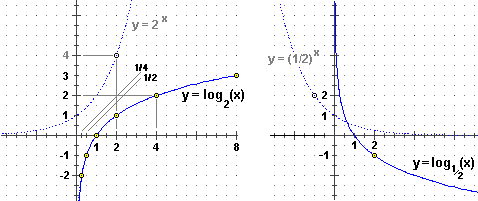
  Il grafico soprastante a sinistra è, in particolare, quello del logaritmo binario, ossia in base 2; il logaritmo binario non è altro che un'estensione del concetto di ordine di grandezza riferito alla scrittura binaria dei numeri: in base 2, 8 = 2³ ha ordine di grandezza 3, ovvero log₂(8) = 3, e infatti si scrive (1000)₂ (la prima cifra ha posto 3);  1090 = 1024 + 64 + 2 = 2¹⁰+2⁶+2¹ = (10001000010)₂ (la prima ha posto 10).
    Così come gli ordini di grandezza possono essere grandi a piacere, così sono grandi a piacere i logaritmi in base 10, in base 2 e in ogni base maggiore di 1, ossia i loro grafici salgono oltre ogni limite. Possono anche essere negativi con valore assoluto grande a piacere (1 millesimo ha ordine di grandezza -3, 1 miliardesimo -9, …). Simbolicamente, se a > 1:

lim_{x → ∞} log_a(x) = ∞   lim_{x → 0+} log_a(x) = –∞

In accordo col fatto che le funzioni inverse hanno grafici simmetrici rispetto a y=x abbiamo:

lim_{x → ∞} a^x = ∞   lim_{x → –∞} a^x = 0

Se 0 < a < 1 il comportamento del logaritmo [dell'esponenziale] è simmetrico rispetto all'asse x [all'asse y] rispetto al caso a>1, come è evidenziato dal grafico soprastante a destra:

lim_{x → ∞} log_a(x) = –∞   lim_{x → 0+} log_a(x) = ∞

lim_{x → ∞} a^x = 0   lim_{x → –∞} a^x = ∞

  Dalle proprietà delle potenze discendono particolari proprietà dei logaritmi. In particolare:
• dal fatto che a^b+c = a^b·a^c, ossia che x a^x trasforma la somma di due input nel prodotto degli output, segue che la funzione inversa trasforma, inversamente, il prodotto degli input nella somma degli output:

log_a(p · q) = log_a(p) + log_a(q)

Ad esempio il ragionamento con cui si trasforma 1000·100 è in 10²⁺³ può essere interpretato così:  "a che cosa devo elevare 10 per ottenere 1000·100? alla somma degli esponenti a cui lo elevo per ottenere 1000 e 100", ossia:  Log(1000·100) = Log(1000)+Log(100).
• dal fatto che a^-b = 1/a^b, ossia che x a^x trasforma l'opposto di un input nel reciproco dell'output, segue che la funzione inversa trasforma, inversamente, il reciproco di un input nell'opposto dell'output:

log_a(1/q) = – log_a(q)

Ad esempio:  "a che cosa devo elevare 10 per ottenere 1/1000? all'opposto del numero a cui lo elevo per ottenere 1000", ossia:  Log(1/1000) = –Log(1000) = –3.
• dal fatto che a^b–c = a^b/a^c, ossia che x a^x trasforma la differenza di due input nel rapporto degli output, segue che la funzione inversa trasforma, inversamente, il rapporto degli input nella differenza degli output:

log_a(p / q) = log_a(p) – log_a(q)

• Che cosa possiamo dire di  log_a(p³)?
Usando la prima formula riportata in questo punto abbiamo:  log_a(p³) = log_a(p·p·p) = log_a(p) + log_a(p)+log_a(p) = 3 · log_a(p).  In generale si ha:

log_a(p^q) = q · log_a(p)

anche se q non è intero; questa formula corrisponde alla proprietà delle potenze  a^b·c = (a^b)^c.

Esercizio  (e soluzione)

 Da come è la derivata delle funzioni esponenziali possiamo ricavare come è quella delle loro funzioni inverse. In particolare:

D(log)(x) = 1/x Infatti D(log)(x) è la pendenza della tangente r al grafico della funzione log nel punto di ascissa x; nella figura a lato abbiamo indicato con y l'ordinata log(x) di tale punto. 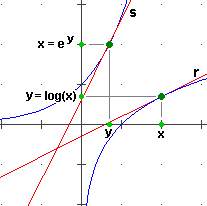Il grafico della funzione inversa (x ex) ha ascisse e ordinate scambiate; la pendenza da noi cercata è quindi il reciproco di quella della tangente s a questo grafico nel punto (y,x). s ha pendenza pari alla derivata di x ex in y; la derivata di questa funzione coincide con la funzione stessa, quindi la pendenza di s è ey. Ma ey = x, e 1/x è dunque la pendenza di r . In breve:   Dx(log(x)) = 1 / Dy(ey) = 1/ey = 1/x.

    Il logaritmo naturale è quello che ha la derivata con l'espressione più semplice. Le derivate delle altre funzioni logaritmiche possono essere ricondotte a questa. Un modo semplice per farlo è ricorrere a un trucco che risulta essere comodo in molte occasioni: usare opportunamente le trasformazioni  x = e^log(x)  e  log(p^q) = q·log(p).
    Vediamo, dunque, come esprime un logaritmo in una base generica mediante i logaritmi naturali:

log_a(x) = log_a(e^log(x)) = log(x)·log_a(e)

per esprimere log_a(e) usando solo log basta pensare al significato del logaritmo:
k = log_a(e) significa che a^k = e, ossia, elevando a 1/k, che a = e^1/k, ossia che log(a) = 1/k, ossia che log_a(e) = k = 1/log(a). Quindi:

log_a(x) = log(x) / log(a)

In definitiva, usando le proprietà di base delle derivate:

D_x(log_a(x)) = D_x(log(x)/log(a)) = D_x(log(x)) / log(a) = 1/(x·log(a))

  Infiniti e infinitesimi, ed esponenziali e logaritmi

    Mentre x e^x ha derivata che varia proporzionalmente all'output, la sua inversa, log, ha derivata che varia in modo inversamente proporzionale all'input.
    Ciò corrisponde al fatto che, per x → ∞, e^x è un infinito che cresce molto velocemente, mentre log(x) è infinito che cresce molto lentamente (la pendenza del grafico tende rapidamente a 0).

    Si può in effetti dimostrare che x x^α, qualunque sia α > 0, cresce più lentamente di exp e più velocemente di log.  In simboli, per ogni α > 0:

lim_{x → ∞} e^x / x^α = ∞     lim_{x → ∞} log(x) / x^α = 0

A fianco, ad esempio, si vede che y = x4 dopo aver scavalcato y = exp(x) e un primo andamento che sembra far pensare che continui a crescere sempre più velocemente dell'esponenziale, in realtà, a un certo punto, per un input di poco superiore ad 8, viene scavalcata dalla curva y = exp(x).   Per convincersi che vale in generale, ossia che exp(x) > xα da un certo punto in poi qualunque sia α positivo, è più comodo ragionare sul grafico della funzione logaritmo. Infatti, per x > 0: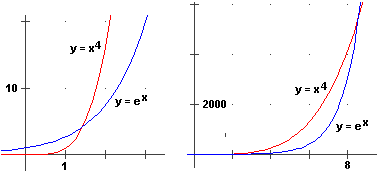

ex > xα   equivale (essendo log crescente) a:   x = log(ex) > log(xα) = α log(x)   ossia (essendo α > 0) a:   x / α > log(x)  e certamente esiste k tale che, per ogni x > k questa disequazione sia vera. Infatti il grafico di log ha pendenza che tende a 0 mentre y = x/α è una retta con pendenza 1/α > 0, che da un certo punto in poi sicuramente sta sopra ad esso. A fianco è illustrato il caso α = 4.

    Queste considerazioni si estendono alle altre funzioni esponenziali e logaritmiche di base maggiore di 1 in quanto i loro grafici hanno lo stesso andamento o, meglio, sono ottenibili da quelli di exp e di log mediante trasformazioni di scala. Dunque, per ogni a > 1 e ogni α > 0, abbiamo che, per x → ∞, a^x è un infinito di ordine superiore rispetto a x^α e log _a(x) è un infinito di ordine inferiore rispetto a x^α.  In simboli [ infiniti e infinitesimi]:

se a>1  e  α>0,  per x → ∞  x^α = o(a^x)   e  log_a(x) = o(x^α)

• Esempio:  lim_{x → ∞} (2^x + x⁸ + 3) / (5^x – 7x) = lim_{x → ∞} (2^x + o(2^x)) / (5^x + o(5^x)) = lim_{x → ∞} 2^x / 5^x = lim_{x → ∞} 0.2^x = 0
In breve, nel rapporto abbiamo trascurato i termini additivi con ordine di infinito inferiore e ci siamo ricondotti al limite di una esponenziale con base minore di 1.

• Altro esempio:  lim_{x → –∞} 3^x / (1/x) = lim_{u → ∞} 3^–u / (–1/u) = lim_{u → ∞} – u / 3^u = 0
In breve, con un cambiamento di variabile [ limiti], ci siamo ricondotti al confronto per u → ∞ tra 3^u e u, dei quali sappiamo che il secondo è trascurabile, per cui u/3^u → 0.

In modo del tutto analogo a quanto fatto nel secondo esempio possiamo dimostrare che, se a>1, ax per x → –∞ (ovvero a–x per x → ∞) è un infinitesimo di ordine superiore rispetto a 1/xα, comunque si prenda α positivo.     Ad es. a lato si vede come la curva y=1/x4 che inzialmente si avvicina maggiormente all'asse x, prima o poi viene scavalcata da  y = exp(-x), che poi continua a spiaccicarsi sempre più velocemente sull'asse y. • Ulteriore esempio:  limx → ∞ (x + log(x)) / (3x + 1) = limx → ∞ (x + o(x)) / (3x + o(x)) = limx → ∞ x / (3x) = limx → ∞ 1/3 = 1/3 In breve, nel rapporto abbiamo trascurato, nel primo termine, log(x) che per x → ∞ è trascurabile rispetto a x e, nel secondo, 1 che è trascurabile rispetto a 3x.

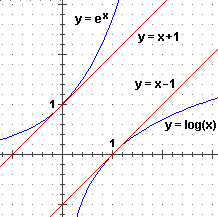Il fatto che il grafico di exp abbia in (0,1) come tangente y = x+1 ci assicura [ infiniti e infinitesimi] che per x → 0  ex = x + 1 + o(x)  ovvero  ex−1 ≈ x.     Per simmetria, y = x−1 è la tangente al grafico di log in (1,0) e, per x → 1,  log(x) = x – 1 + o(x−1)  ovvero  log(x) ≈ x−1 • Esempio:   limx → 1 log(x) / (x2 – 1) = limx → 1(x–1+o(x–1)) / ((x–1)(x+1)) = limx → 1(x–1) / ((x–1)(x+1)) = limx → 11/ (x+1) = 1/2. • Altro esempio:   limx → 0 (10x – ex)/sin(x) = limx → 0(log(10)x+1 – (x+1) + o(x)) / (x + o(x)) = limx → 0(log(10)–1)x / x = log(10)–1.

Il fatto che 10^x = log(10)x+1+o(x) può essere dedotto in più modi.
Ad esempio si può ricordare che D_x(10^x) = log(10)10^x e che quindi la tangente in (0,1) è y = log(10)x+1.
Oppure si può usare il trucco:  10^x = exp(log(10^x)) = exp(x log(10)), e da exp(u) = u+1+o(u) dedurre (ponendo u = x log(10)) che exp(x log(10)) = x log(10)+1+o(x).

Esercizio (e soluzione)

 Equazioni e disequazioni con esponenziali e logaritmi

    La risoluzione di equazioni e disequazioni che coinvolgono le funzioni discusse in questa voce non comporta problemi nuovi, se non quelli legati alle caratteristiche di queste funzioni. Basterà fare qualche esempio:

• Risolvere rispetto a x     3 x2 – 2x = 1/3
log3(3 x2 – 2x) = log3(1/3)		ho applicato la funzione inversa di x 3x
x2 – 2x = –1		ho tenuto conto che 1/3 = 3-1
x2 – 2x + 1 = 0
(x – 1)2 = 0
x = 1		[verifica: 31-2 = 3-1 = 1/3: OK]

• Risolvere rispetto a x     log 3 √x = 2
√x = 32		ho applicato la funzione inversa di x log3(x)
x = (32)2		ho applicato la funzione inversa di x √x
x = 92 = 81		[verifica: log3√81 = log39 = 2: OK]

• Risolvere rispetto a x     log x 5 = 3
x3 = 5		logab = c  quando  ac = b
x =51/3		ho applicato la funzione inversa di x x3
x = 3√5 = 1.70997…	[verifica: log 51/3 5 = 3: OK]

• Risolvere rispetto a x     log(2x-5) > log(7-2x)
La disequazione è definita quando 2x-5>0 & 7-2x>0, ossia x>5/2 & x<7/2
2x-5 > 7-2x		ho applicato x ex, che è crescente
x > 3		ho aggiunto ai due membri 2x, poi 5 e poi ho diviso per 4
3 < x < 7/2		ho tenuto conto del dominio e del fatto che 3 > 5/2

• Risolvere rispetto a x     log(x2 – 2) ≤ log(x)
La disequazione è definita quando x2>2 & x>0, ossia x>√2
x2 – 2 ≤ x		ho applicato x ex, che è crescente
x2 – x – 2 ≤ 0
(x – 1/2)2– 1/4 – 2 ≤ 0		ho completato il quadrato
(x – 1/2)2 ≤ 9/4
-3/2+1/2 ≤ x ≤ 3/2+1/2
√2 < x ≤ 2		ho tenuto conto del dominio
[invece di completare il quadrato potevo osservare subito che x2 – x – 2 si azzera per x=2, fare la divisione per x-2, ottenere x+1, dedurre la scomposizione (x-2)(x+1); oppure potevo usare la formula per esprimere le eventuali soluzioni di una equazione polinomiale di 2° grado: x = 1/2 ± √(1+8)/2 = 1/2 ± 3/2; in entrambi i casi deducevo che y = x2–x–2 è una parabola con la concavità verso l'alto che sta sotto l'asse x tra -1 e 2]

 Nota 1.  A volte (come in alcuni degli esempi precedenti) si usa  log x  al posto di log(x). Per questa "notazione abbreviata" valgono considerazioni critiche e attenzioni da prestare simili a quelle discusse a proposito delle analoghe notazioni usate con sin, cos, tan.

 Nota 2.  x → log(e^x)  e  x → e^log(x), pur essendo il logaritmo la funzione inversa dell'esponenziale, non sono la stessa funzione:  la prima è definita per ogni input (equivale alla funzione identità x → x), mentre la seconda è definita solo per input positivi (equivale alla funzione identità ristretta agli input positivi), in quanto log(x) è definito solo per x numero reale positivo. La prima ha per grafico la retta bisettrice del I e III quadrante, la seconda ha per grafico la semiretta bisettrice del I.

Esercizi:  

 altri collegamenti     [nuova pagina]