I principali Teoremi del Calcolo
Differenziale
Argomenti:
[1] Teorema di Rolle
[2] Teorema di Lagrange
[2.1] Corollario
1
[2.2] Corollario
2
[2.3] Corollario
3
[3] Teorema di Cauchy
[4] Osservazioni sui Teoremi
[4.1]
sul teorema di Rolle
[4.2]
sul teorema di Lagrange
[1] Teorema di Rolle
Sia f una funzione continua in un intervallo chiuso [a, b] e derivabile
in (a, b) tale che f(a)=f(b). Allora esiste x
in (a, b) tale che f ' (x)=0
Interpretazione geometrica: Sotto le opportune
ipotesi di continuità e di derivabilità che sono state enunciate,
se f(a)=f(b), allora esiste x in (a, b) tale
che la tangente al grafico nel punto di coordinate (x
, f(x)) sia orizzontale.
N.B.: L'ipotesi di continuità su tutto l'intervallo chiuso è
fondamentale: a questo proposito si veda l'esempio
Inizio pagina
[2] Teorema di Lagrange
Sia f una funzione continua in un intervallo chiuso [a, b] e derivabile
in (a, b). Allora esiste x in (a, b) tale che
Interpretazione geometrica: Sotto le opportune
ipotesi di continuità e di derivabilità che sono state enunciate,
esiste x in (a, b) tale che la tangente al grafico
nel punto di coordinate (x , f(x))
sia parallela alla retta che congiunge i punti di coordinate (a, f(a))
e (b, f(b)).
N.B.: Il Teorema di Rolle è un caso
particolare del Teorema di Lagrange nel caso in cui f(a)=f(b). Il teorema
di Lagrange si dimostra riconducendosi al teorema di Rolle.
Inizio pagina
[2.1] Corollario 1
Sia f una funzione continua in un intervallo chiuso [a, b] e derivabile
in (a, b) tale che f '(x)=0 per ogni x in (a, b). Allora esiste un numero
reale k tale che f(x)=k per ogni x in [a,b], cioè' f e' costante
su tutto il dominio di definizione.
Inizio pagina
[2.2] Corollario 2
Siano f e g due funzioni continue in un intervallo chiuso [a,
b] e derivabili in (a, b) tali che f '(x)=g'(x) per ogni x in (a, b). Allora
esiste un numero reale c tale che f(x)=g(x)+c per ogni x in [a,b], cioè
f e g differiscono a meno di una costante.
Inizio pagina
[2.3] Corollario 3
Sia f una funzione continua in un intervallo chiuso [a, b] e derivabile
in (a, b). Allora:
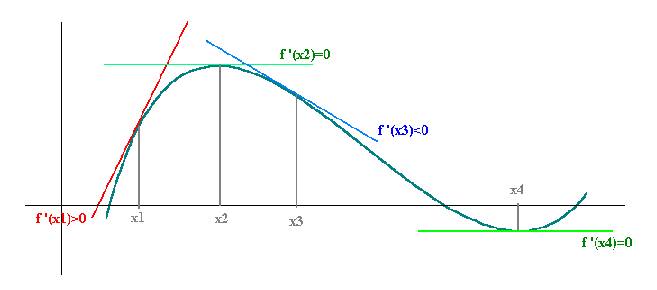
i) Se f '(x)>0 per ogni x in (a, b), allora f è
crescente in [a, b].
ii) Se f '(x)<0 per ogni x in (a, b), allora f
è decrescente [a, b].
Tale corollario è importantissimo ed ha un ruolo determinante
nella ricerca dei punti di estremo relativo di
una funzione.
Dal punto di vista intuitivo:
:
Inizio pagina
[3] Teorema di Cauchy
Siano f e g due funzioni continue in un intervallo chiuso [a,
b] e derivabili in (a, b). Se g '(x)<>0 per ogni x in (a,b), allora
esiste x in (a, b) tale che
Inizio pagina
[4] Osservazioni sui teoremi
Osservazioni sul teorema di Rolle
Osserviamo che l'ipotesi di continuità della funzione su tutto l'intervallo
chiuso [a, b] è fondamentale (vai a: Teorema
di Rolle). Supponiamo infatti che la funzione f sia continua e derivabile
su (a, b) ma che presenti una discontinuità negli estremi a e b.
In tal caso la funzione potrebbe non essere costante sull'intervallo: consideriamo
ad esempio la seguente funzione:
Come si può notare, la funzione della figura, a parte la continuità
negli estremi, gode di tutte le altre proprietà elencate dall'enunciato
del teorema di Rolle. Come si può notare, essa non è costante.
Inizio pagina
[4.2] Osservazioni sul teorema
di Lagrange
Il Teorema di Lagrange si dimostra riconducendosi
al Teorema di Rolle: si consideri infatti la funzione
g definita da:
Dal punto di vista geometrico, il grafico della funzione g è il
grafico di f che è stato fatto ruotare di un opportuno angolo, in
modo da rendere orizzontale la congiungente dei punti (a, f(a)), (b, f(b)).
La funzione g verifica le ipotesi del Teorema di Rolle e dunque esiste
x in (a, b) tale che g ' (x)=0,
cioè esiste x in (a, b) tale che
cioè la tesi.
Inizio pagina
Collegamenti
Definizione di derivata
Interpretazione geometrica del concetto di
derivata
Definizione di tangente ad una curva
Coefficiente direttivo di una retta e
tangente trigonometrica
Derivata in un punto e funzione derivata
Massimi e minimi
Ricerca di massimi e di minimi
Regole di derivazione