Strutture numeriche
 Si parla di struttura
numerica quando congiuntamente a un insieme numerico
(numeri reali, numeri interi, numeri naturali, numeri periodici,
numeri decimali limitati, …) si considerano uno o
più oggetti matematici che stabiliscano dei collegamenti tra i
vari numeri.
Si parla di struttura
numerica quando congiuntamente a un insieme numerico
(numeri reali, numeri interi, numeri naturali, numeri periodici,
numeri decimali limitati, …) si considerano uno o
più oggetti matematici che stabiliscano dei collegamenti tra i
vari numeri.
|
Ad esempio, se voglio
un modello matematico che mi consenta di stabilire se due quantità
di oggetti sono uguali, posso utilizzare i numeri naturali dotati
della funzione successore S, che a ogni numero naturale n associa il numero
successivo (il numero su cui un  contatore posizionato su n
si posiziona ad un nuovo scatto): contatore posizionato su n
si posiziona ad un nuovo scatto):
– a partire da 0
per ogni oggetto della prima collezione applico una volta S;
– a
partire da 0 faccio la stessa cosa con gli oggetti della seconda
collezione;
– se i due output
finali sono uguali posso concludere che le due quantità sono
uguali. |
 |
Se, invece, voglio
stabilire la quantità complessiva di oggetti che ottengo
mettendo insieme due quantità note posso utilizzare come
modello matematico i numeri naturali dotati della funzione di
addizione.
|
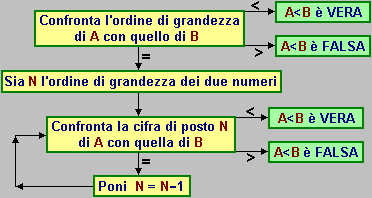
Se voglio confrontare
delle misure di lunghezza posso considerare l'insieme dei numeri
reali positivi dotato della relazione di ordine "<".
Questa
può essere definita ricorrendo a un confronto cifra per
cifra, cioè nel modo illustrato a fianco:
|
 |
 Le "quattro
operazioni" tra numeri interi sono
tutte facilmente definibili a partire dalla funzione successore e
dalla sua funzione inversa, la funzione predecessore: Le "quattro
operazioni" tra numeri interi sono
tutte facilmente definibili a partire dalla funzione successore e
dalla sua funzione inversa, la funzione predecessore:
– per
addizionare un numero positivo n a un numero intero
applico n volte la funzione successore, mentre per
sottrarre il numero positivo n (ovvero per addizionare –n)
applico n volte la funzione predecessore.
|
 |
– per moltiplicare
posso procedere ripetendo addizioni; per dividere posso
procedere ripetendo sottrazioni: «quante volte 2 sta nel 15?»
equivale a «a partire da 15 quante volte posso ripetere la
sottrazione di 2 prima di arrivare a un risultato negativo?».
|
Alla scuola elementare
si impara come ricondurre le operazioni tra numeri decimali
limitati a operazioni tra numeri
interi; ad esempio 3.5+2.4 viene
calcolata così:
3.5 + 2.4  35 decimi + 24 decimi
35 decimi + 24 decimi  59 decimi
59 decimi  5.9;
5.9;
0.24 / 0.7 viene
calcolata così:
2.4 / 0.7  24 decimi / 7 decimi
24 decimi / 7 decimi  24/7
24/7  3 con resto 3 (ovvero 3.428…; più
3 con resto 3 (ovvero 3.428…; più  avanti è richiamato come
proseguire la divisione ottenendo un risultato non intero)
avanti è richiamato come
proseguire la divisione ottenendo un risultato non intero)
Come possiamo estendere
le quattro operazioni agli altri numeri reali?
Un'operazione tra numeri
reali x e y che non siano decimali limitati viene
ricondotta all'esecuzione della stessa operazione su intervalli che
contengano x e y e abbiano estremi decimali limitati.
Consideriamo
l'addizione.
• Se
so che due aste hanno lunghezze in cm x e y comprese,
rispettivamente, tra 1.3 e 1.4 e tra 1.1 e 1.2, volendo che x+y
sia la lunghezza in cm dell'asta che si ottiene congiungendo le due
aste precedenti, dovrò avere: 1.3+1.1 ≤ x+y
≤ 1.4+1.2, cioè: x+y  [2.4, 2.6],
intervallo ampio 0.2; [per "
[2.4, 2.6],
intervallo ampio 0.2; [per " ":
":  ]
]

• se
approssimo x e y con intervalli di ampiezza pari a un
decimo di quella dei precedenti, ad es. se x  [1.35, 1.36] e y
[1.35, 1.36] e y  [1.12, 1.13], devo avere: x+y
[1.12, 1.13], devo avere: x+y  [2.47, 2.49], intervallo ampio 0.02;
[2.47, 2.49], intervallo ampio 0.02;
• più
in generale, se divido per 10 l'ampiezza degli intervalli con cui
approssimo x e y, anche l'ampiezza dell'intervallo in
cui deve cadere x+y si divide per 10.
Quindi, migliorando
la precisione con cui conosco x e y (cioè
aumentando il numero di cifre con cui approssimo x e y)
posso migliorare quanto voglio la precisione con cui conosco x+y.
Considerazioni
simili si possono fare per moltiplicazione, sottrazione e divisione.
In modi abbastanza
simili si possono definire anche altre operazioni. Ad esempio abbiamo
visto che l'estrazione della radice quadrata di y
può essere definita mediante un procedimento che mi permette
di trovare una dopo l'altra le cifre di un numero (non negativo) x tale che
x·x=y [ ].
].
Analogamente si può
definire n√y (radice ennesima) mediante un  procedimento numerico per risolvere l'equazione xn = y (con la condizione 0 ≤ x nel caso in cui n sia pari).
procedimento numerico per risolvere l'equazione xn = y (con la condizione 0 ≤ x nel caso in cui n sia pari).
 Nota. Ora
possiamo precisare come
Nota. Ora
possiamo precisare come  l'elevamento a potenza
si estende agli esponenti non interi.
l'elevamento a potenza
si estende agli esponenti non interi.
Si è già
visto il caso degli esponenti decimali limitati:
20.4 =
24/10 = 22/5 = 22·(1/5) = 5√(22) = 5√4 =
1.3195…
[ l'esponente viene espresso come frazione m/n  irriducibile e poi pensato come m·(1/n), in modo da ottenere:
irriducibile e poi pensato come m·(1/n), in modo da ottenere:
am/n → am(1/n) → (am)(1/n) = n√(am) ]
Consideriamo, ad esempio,
23.413691375…. Possiamo calcolare:
|
23 = 8 | 24 = 16 |
|
23.4 =
234/10 = 217/5 = 5√217 = 10.5560… | 23.5 = 235/10 = 27/2 = 2√27 =
11.3137… |
| 23.41 =
2341/100 = 100√2341 = 10.6294… |
23.42 = … = 10.7304… |
| 23.413
= … = 10.6516… | 23.414 = … =
10.6589… |
| … | … |
| 23.4136913
= … = 10.6567180… | 23.4136914 = …
= 10.6567188… |
Si ottiene una
successione di intervalli [8, 16], [10.5560…, 11.3137…],
[10.6294…, 10.7304…], … di ampiezza sempre più
piccola, che consente di approssimare 23.413691375…
con la precisione che si vuole. Ad es. in base ai calcoli sopra effettuati possiamo concludere che 10.656718 ne è la approssimazione per troncamento con 8 cifre significative.
Una calcolatrice dotata del tasto  o, in genere, il software (usando il simbolo "^") effettuano il calcolo
non seguendo direttamente questo procedimento, ma con un algoritmo più efficiente, così come usano un algortimo per la radice quadrata
più efficiente di quello con cui l'abbiamo definita.
o, in genere, il software (usando il simbolo "^") effettuano il calcolo
non seguendo direttamente questo procedimento, ma con un algoritmo più efficiente, così come usano un algortimo per la radice quadrata
più efficiente di quello con cui l'abbiamo definita.
Tuttavia, come abbiamo  osservato, il software non svolge il calcolo di (−8)^(1/3), che fa −2, ossia non svolge in alcun caso il calcolo di x^y quando x è negativo;
nel caso della radice cubica di x per avere il risultato anche quando x è negativo occorre battere abs(x)^(1/3)*sign(x).
osservato, il software non svolge il calcolo di (−8)^(1/3), che fa −2, ossia non svolge in alcun caso il calcolo di x^y quando x è negativo;
nel caso della radice cubica di x per avere il risultato anche quando x è negativo occorre battere abs(x)^(1/3)*sign(x).
 Le definizioni delle
relazioni e delle operazioni tra numeri reali che abbiamo dato
(relazione d'ordine (<), addizione, moltiplicazione, … ) sono
state scelte in modo che la struttura numerica che si ottiene possa
essere utilizzata come modello matematico per rappresentare misure,
confronti e operazioni tra grandezze fisiche. Si può
dimostrare che per questa struttura valgono le proprietà
algebriche che abbiamo utilizzato per trasformare termini ed
equazioni. [
Le definizioni delle
relazioni e delle operazioni tra numeri reali che abbiamo dato
(relazione d'ordine (<), addizione, moltiplicazione, … ) sono
state scelte in modo che la struttura numerica che si ottiene possa
essere utilizzata come modello matematico per rappresentare misure,
confronti e operazioni tra grandezze fisiche. Si può
dimostrare che per questa struttura valgono le proprietà
algebriche che abbiamo utilizzato per trasformare termini ed
equazioni. [ termini equivalenti]
termini equivalenti]
|
 Operazioni e
relazioni possono anche essere definite diversamente.
Consideriamo ad esempio un'asta imperniata per un'estremità
al centro di un disco graduato e inizialmente nella posizione 0°.
Se voglio costruire un modello matematico per rappresentare quale
posizione essa raggiunge quando viene soggetta a due successive
rotazioni antiorarie, posso utilizzare una nuova operazione che ai
valori (in gradi) della prima e della seconda rotazione associa la
posizione finale (in gradi) dell'asta. Operazioni e
relazioni possono anche essere definite diversamente.
Consideriamo ad esempio un'asta imperniata per un'estremità
al centro di un disco graduato e inizialmente nella posizione 0°.
Se voglio costruire un modello matematico per rappresentare quale
posizione essa raggiunge quando viene soggetta a due successive
rotazioni antiorarie, posso utilizzare una nuova operazione che ai
valori (in gradi) della prima e della seconda rotazione associa la
posizione finale (in gradi) dell'asta.
|
 |
|
Indichiamo con il
simbolo (+) questa operazione, che ha input e output
nell'intervallo di numeri reali [0,360).
Come nel caso
dell'usuale addizione, abbiamo, ad esempio, che 180 (+) 90 fa 270.
Anche
90 (+) 180 fa 270. |

180(+)90 = 270 |
| Più in generale
vale la proprietà x(+)y = y(+)x, così come valgono altre
proprietà dell'usuale addizione: |
• x(+)0 = x,
• esiste
y tale che x(+)y = 0 (y è la rotazione che riporta l'asta
dalla posizione x alla posizione 0),
• …
Tuttavia
non vale la proprietà: «0 è l'unico numero
che sommato a se stesso dà come risultato 0», cioè:
«l'equazione x+x = 0 ha come unica soluzione x = 0».
Infatti
abbiamo sia 0 (+) 0 = 0 che 180 (+) 180 = 0. |

180(+)180 = 0 |
Anche l'intervallo
[0,360) dotato dell'operazione (+) è una struttura
numerica, pur se non verifica tutte le proprietà
algebriche che valgono per l'insieme di tutti i numeri reali dotato
dell'usuale addizione.
Analogamente l'insieme {0,1,2,…11} dotato dell'operazione (+)
che a due ore associa l'ora "somma", (3,7) → 10, (8,7) → 3, è
una struttura numerica.
Nota.
Ecco come definire in R tali operazioni, usando la funzione "resto intero" %%:
piu <- function(x,y) (x+y)%%360
piu2 <- function(x,y) (x+y)%%12
Se batto piu(180,270) ottengo 90.
Si usa anche dire che 350 (= 180+270) e 90 sono equivalenti modulo 360 per esprimere
che sono eguali a meno di multipli di 360, così come 6, 18, 30, 42 sono equivalenti modulo 12 (se a partire
dalle ore 6 aggiungo 12, 12·2, 12·3 ottengo sempre la stessa ora su un orologio a lancette).
Vedi in fondo a questa voce come caricare in R un file che esegue questo ed altri calcoli più facilmente.
 Vi sono situazioni in cui può essere utile ricorre a strutture
definite su un sottoinsieme dei numeri naturali. Ad esempio per tener conto dell'ordine di arrivo degli utenti ad uno sportello (bancario, postale, …) o in un negozio usualmente molto affollato si può ricorrere alla distribuzione automatica di biglietti numerati da 01 a 99; arrivato al biglietto 99 il distributore riparte con un biglietto numero 01, poi numero 02, …. Abbiamo una struttura numerica simile a quella considerata
Vi sono situazioni in cui può essere utile ricorre a strutture
definite su un sottoinsieme dei numeri naturali. Ad esempio per tener conto dell'ordine di arrivo degli utenti ad uno sportello (bancario, postale, …) o in un negozio usualmente molto affollato si può ricorrere alla distribuzione automatica di biglietti numerati da 01 a 99; arrivato al biglietto 99 il distributore riparte con un biglietto numero 01, poi numero 02, …. Abbiamo una struttura numerica simile a quella considerata  all'inizio della voce, ma con al posto di S una funzione-successore differente, chiamiamola S', così definita: S'(01)=02, S'(02)=03, …, S'(99)=01. Definendo un'addizione (+) mediante questa funzione-successore abbiamo ad esempio 88(+)20 = 09 (avanzando di 11 si arriva a 99, con altri 9 si arriva a 09).
all'inizio della voce, ma con al posto di S una funzione-successore differente, chiamiamola S', così definita: S'(01)=02, S'(02)=03, …, S'(99)=01. Definendo un'addizione (+) mediante questa funzione-successore abbiamo ad esempio 88(+)20 = 09 (avanzando di 11 si arriva a 99, con altri 9 si arriva a 09).
Simili sono la struttura dei numeri delle ore sull'orologio (a 12 segue 1) e quella dei giorni della settimana (LU  MA
MA  ME
ME  GI
GI  VE
VE  SA
SA  DO
DO  LU
LU  …).
…).
Ovvero, si pensi la struttura costutuita dalle cifre di un  contagiri. Nel contatore decimale abbiamo: 0
contagiri. Nel contatore decimale abbiamo: 0  1
1  2
2  …
…  8
8  9
9  0
0  1
1  …. In quello binario: 0
…. In quello binario: 0  1
1  0
0  1
1  0
0  ….
….
 Addizionando, sottraendo
e moltiplicando numeri interi otteniamo sempre numeri interi.
Addizionando, sottraendo e moltiplicando numeri decimali limitati
otteniamo sempre numeri decimali limitati.
Addizionando, sottraendo
e moltiplicando numeri interi otteniamo sempre numeri interi.
Addizionando, sottraendo e moltiplicando numeri decimali limitati
otteniamo sempre numeri decimali limitati.
Ciò si può
esprimere dicendo che l'insieme dei numeri interi e quello dei numeri
decimali limitati sono chiusi rispetto all'addizione,
alla sottrazione e alla moltiplicazione.
La divisione tra numeri
interi in alcuni casi dà risultato intero, in altri no: 1/3 fa
0.333…, che non è intero. Questo esempio ci mostra che lo stesso
accade anche per i numeri decimali limitati: 1 e 3 sono decimali
limitati, 0.333… no. Quindi questi due insiemi non sono chiusi rispetto
alla divisione.
E i numeri
periodici?
•
Ogni
numero periodico è esprimibile come risultato della divisione
tra numeri interi.
Infatti, come si può verificare facilmente con una CT, dividendo 7 per 9 ottengo 0.777…, 23 per 99 ottengo 0.232323…, 81 per 999 ottengo 0.081081081… e, più in generale, dividendo un numero naturale per 99…9 (sequenza di n 9) si ottiene
un numero con periodo di n cifre; più precisamente si ottiene il periodo c1c2…cn se si divide c1c2…cn per 99…9. Quindi:
—— 83 ———— 0254
0.83 = —— 0.0254 = ————
99 9999
—— —— 71 63·99 71 6237+71 6308
63.71 = 63 + 0.71 = 63 + —— = ————— + —— = ——————— = ————
99 99 99 99 99
—— —— 1 6308 1 6308
6.371 = 63.71 · —— = ———— · —— = ————
10 99 10 990
Nota. Fino alla prima metà del XX secolo, quando non erano diffusi i mezzi di calcolo, poteva essere utile,
per chi doveva fare spesso calcoli, ricorrere a un procedimento per trasformare numeri periodici in rapporti tra interi più
meccanico (*), ma che le persone, se non mantenevano l'allenamento, dimenticavano facilmente. In qualche "vecchio" libro di scuola si trovano ancora cose di questo genere.
(*) per chi ha voglia di leggerlo era il seguente: "un numero periodico è generato dlla frazione avente come numeratore
la differenza tra il numero formato da tutte le cifre che precedono il periodo seguite da quelle del periodo e il numero formato dalle cifre che
precedono il periodo e come denominatore il numero formato da tanti 9 quante sono le cifre del periodo e tanti zeri quante sono le cifre
dell'antiperiodo" !!! ; nell'ultimo caso, il procedimento avrebbe portato direttamente al calcolo di (6371-63)/990.
• E, viceversa, ogni
divisione tra numeri interi (quando è definita, cioè
quando il secondo termine della divisione non è 0) ha come
risultato un numero periodico .
Per capirlo consideriamo, ad es., 24/7. Il risultato intero è 3 (7·3=21) con il resto di 3 (24-21=3). Per trovare la parte decimale si prosegue dividendo 3 per 7 mediante la trasformazione di 3 in 30 decimi. Facendo 30/7 si trova 4 con il resto di 2. Quindi il risultato è 3 e 4 decimi. Per trovare un'ulteriore cifra si trasformano i 2 decimi di resto in 20 centesimi e si fa 20/7: 2 con il resto di 6. Quindi il risultato è 3, 4 decimi e 2 centesimi. Ecc.
3 30 7·4+2 2
— —> —— decimi —> ————— decimi —> 4 + — decimi
7 7 7 7
2 20 7·2+6 6
— decimi —> —— centesimi —> ————— cent. —> 2 + — centesimi
7 7 7 7 |
3 | 7
— |—————————————
30| 0.4285714...
-28
———
20
-14
———
60
-56
———
40
-35
———
50
-49
——
10
-7
———
30
-28
———
20
... |
L'algoritmo per trovare la parte decimale è usualmente schematizzato nel modo a fianco: man mano si calcola il risultato intero, si trova il resto e gli si aggiunge "0", si trova il nuovo risultato intero e il nuovo resto, e così via.
I resti possibili di una divisione per 7 sono 0, 1, 2, 3, 4, 5 e 6; quindi prima o poi, dopo al più 7 passi, si incontra un resto già trovato. E infatti, in questo caso, si ritrova 3. Da lì in poi il procedimento si ripete esattamente come prima. Il risultato esatto è quindi un numero periodico, con periodo (428571) lungo 6. Una divisione di un numero intero per 7 può dare un numero con periodo lungo al più 6 (infatti come resti si possono susseguire al massimo, in un qualche ordine, i numeri da 1 a 7; se invece si incontra il resto 0, da lì in poi si ripete sempre il resto 0: il risultato è un numero decimale limitato).
Più in generale la divisione tra due interi m/n ha come risultato esatto un numero periodico con periodo lungo al più n (o, in particolare, un numero decimale limitato o, in particolare, intero).
Da QUI puoi accedere a un programma
che calcola la divisione tra due interi esprimendo il risultato
in una base a scelta (l'algoritmo della divisione è lo stesso: in base 60 si trasforma via via il resto in sessantesimi,
ossia si moltiplica per 60 invece che per 10): prova a usarlo per 3/7 sia in base 10 che in base 60 (e verifica
che 3/7 di ora sono 25'43"). |
• Quindi, i numeri
periodici sono identificabili con i numeri esprimibili come rapporto tra due interi (ossia nella forma m/n
con m e n numeri interi), cioè con i cosiddetti
numeri razionali [il termine "razionale" deriva dal fatto che "razione" (ratio, onis) era il termine latino per "rapporto"; da "ragione", parola nata come deformazione di "razione", quando intesa come "rapporto", deriva ragionieria, ossia l'applicazione della matematica elementare - rapporti, proporzionalità, … - ai calcoli di tipo economico].
 Le quattro operazioni
tra numeri razionali hanno sempre risultato razionale (cioè
esprimibile nella forma m/n):
Le quattro operazioni
tra numeri razionali hanno sempre risultato razionale (cioè
esprimibile nella forma m/n):
a c a·d b·c a·d + b·c
— + — = ——— + ——— = —————————
b d b·d b·d b·d
a c a·d b·c a·d - b·c
— - — = ——— - ——— = —————————
b d b·d b·d b·d
a c a·c
— · — = ———
b d b·d
a a
— —·b
b b a a·d a·d
—— = ———— = ——— = ————— = ———
c c c·b c·b c·b
— —·b ——— ———·d ovvero:
d d d d
-1
a c a d a·d
… = —·(—) = —·— = ———
b d b c b·c
[per le riscritture impiegate:  (moltiplicare per uno stesso termine i termini di un rapporto, trasformare un rapporto in prodotto, …) e
(moltiplicare per uno stesso termine i termini di un rapporto, trasformare un rapporto in prodotto, …) e  (raccogliere a fattor comune) alla voce Termini equivalenti]
(raccogliere a fattor comune) alla voce Termini equivalenti]
Quindi l'insieme dei
numeri periodici (ovvero, numeri razionali) è
chiuso rispetto alla "quattro operazioni". Non è
invece chiuso rispetto all'estrazione della radice quadrata; infatti, ad es., √5
[come abbiamo già osservato:  ] non è periodico.
] non è periodico.
Anche altre radici quadrate non sono periodiche, ad es.: √2, √3, …, √p se p è un numero primo (ossia un numero naturale che è multiplo solo di 1 e di sé stesso) diverso da 1.
Infatti il quadrato q di un numero dalla forma m/n non può essere un numero primo diverso da 1:
da (m/n)·(m/n) = (m·m)/(n·n) = q ricavo m·m = q·n·n; dunque m·m è un multiplo di q; se q fosse primo anche m dovrebbe essere un suo multiplo; ma allora avrei m=q·h da cui q·h·q·h=q·n·n e h·q·h=n·n; quindi anche n sarebbe un multiplo di q, contraddicendo il fatto che avrei potuto semplificare m/n in modo che m e n non abbiano divisori comuni diversi da 1.
I numeri reali non periodici, non essendo razionali, vengono detti anche irrazionali (ma ciò non significa che le loro cifre si susseguano in modo caotico, come si potrebbe pensare riferendosi all'uso dell'aggettivo "irrazionale" come "privo di ogni logica":  esempio (e) alla voce I numeri, le cui cifre si susseguono secondo un ben preciso procedimento).
esempio (e) alla voce I numeri, le cui cifre si susseguono secondo un ben preciso procedimento).
Nota. In genere tra i numeri primi non si include il numero 1, essenzialmente per rendere più comodo l'enunciato di alcune proprietà che varrebbero per tutti i numeri primi ma non per 1, in modo da poter evitare l'aggiunta di "diverso da 1", come quella da noi operata sopra.
Un altro es.: quando si dice che "per ogni numero naturale N maggiore di 1 esiste un unica sequenza ordinata di numeri primi il cui prodotto sia N" si intende escludere 1 dai numeri primi, altrimenti accanto alla scomposizione di 12 come 2·2·3 vi sarebbero anche 1·2·2·3, 1·1·2·2·3, …, che potremmo evitare solo mettendo "… primi diversi da 1".
Ma molti matematici includono anche 1 (ad es. lo fanno alcuni dei matematici più famosi del XIX e del XX secolo, come Lebesgue, Lehmer e Aczel).
Quando si legge un libro o un articolo in cui si parla di numeri primi è bene cercare quale
convenzione usa l'autore. E quando si scrive, per chiarezza, potrebbe essere utile aggiungere all'aggettivo "primo",
eventualmente tra parentesi, la specificazione "diverso da 1" o "incluso 1", a seconda dei casi.
Come ottenere le scomposizioni in numeri primi col software R:
n <- 68
k <- 2; while (k<=n) if (n/k==floor(n/k)) {print(k); n <- n/k} else k <- k+1
2 2 17
Vedi in fondo a questa voce come caricare in R un file che esegue questo ed altri calcoli più facilmente.
Vi sono alcuni criteri di divisibilità per stabilire se un numero intero maggiore di 1 può espresso
come prodotto di altri numeri interi maggiori di 1.
Facciamo alcuni esempi, indicando con x|N il fatto che x è un divisore di N ("x divide N"); 2|N se N termina con una cifra pari;
3|N se lo è la somma delle sue cifre; 4|N se lo è il numero formato dalle sue due ultime cifre;
5|N se l'ultima cifra è 0 o 5; 8|N se lo è il numero formato dalle sue tre ultime cifre;
9|N se lo è la somma delle sue cifre;
11|N se lo è se la differenza fra la somma delle cifre di posto pari e la somma delle cifre di posto dispari.
Ad es. 27918 ha come somma delle cifre 9+9+9 e quindi è divisibile per 9.
 Per indicare in modo abbreviato i vari
insiemi numerici si usano spesso alcuni simboli particolari:
R o IR per indicare l'insieme dei reali,
Q o
Per indicare in modo abbreviato i vari
insiemi numerici si usano spesso alcuni simboli particolari:
R o IR per indicare l'insieme dei reali,
Q o 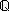 per indicare quello dei numeri razionali,
Z o
per indicare quello dei numeri razionali,
Z o 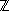 per quello degli interi ("z" è l'inziale della parola che in tedesco significa
"numero") e
N o IN per indicare quello dei numeri naturali.
Si usano anche R*, N*,
… per indicare gli stessi insiemi da cui è stato tolto il numero 0.
per quello degli interi ("z" è l'inziale della parola che in tedesco significa
"numero") e
N o IN per indicare quello dei numeri naturali.
Si usano anche R*, N*,
… per indicare gli stessi insiemi da cui è stato tolto il numero 0.
Questi simboli sono spesso comodi per descrivere domini e immagini di funzioni o, più in generale, l'insieme in cui far variare una variabile. Ad esempio per dire che una funzione è definita per tutti i numeri reali si può dire che ha R, o (- ,
, ), come dominio, per dire che la funzione F: x
), come dominio, per dire che la funzione F: x  x3 è definita per ogni numero e può avere qualunque numero come output possiamo scrivere F(R)=R, per descrivere l'insieme dei numeri interi pari possiamo scrivere 2Z, intendendo indicare l'immagine di Z mediante la funzione x
x3 è definita per ogni numero e può avere qualunque numero come output possiamo scrivere F(R)=R, per descrivere l'insieme dei numeri interi pari possiamo scrivere 2Z, intendendo indicare l'immagine di Z mediante la funzione x  2x, per indicare l'insieme dei numeri razionali compresi tra 0 e 1 (escluso) possiamo scrivere {x
2x, per indicare l'insieme dei numeri razionali compresi tra 0 e 1 (escluso) possiamo scrivere {x Q / 0 ≤ x < 1}.
Q / 0 ≤ x < 1}.
 Nota. Vi è una manipolazione algebrica che prende il nome di razionalizzazione. Con questo termine non si intende la trasformazione di un numero irrazionale in razionale (cosa impossibile, anche cambiando base di rappresentazione, come abbiamo visto), ma semplicemente una manipolazione di un rapporto, in genere operata moltiplicando i due termini del rapporto per uno stesso termine, che lo trasforma in modo da eliminare la comparsa di (tutte o alcune) radici dal secondo termine. Ecco tre esempi:
Nota. Vi è una manipolazione algebrica che prende il nome di razionalizzazione. Con questo termine non si intende la trasformazione di un numero irrazionale in razionale (cosa impossibile, anche cambiando base di rappresentazione, come abbiamo visto), ma semplicemente una manipolazione di un rapporto, in genere operata moltiplicando i due termini del rapporto per uno stesso termine, che lo trasforma in modo da eliminare la comparsa di (tutte o alcune) radici dal secondo termine. Ecco tre esempi:
1 / √3 → √3 / (√3·√3) → √3 / (√3)2 → √3 / 3
(√x + 1) / √x → √x (√x + 1) / (√x·√x) → (x + √x) / x
1 / (√x + 1) → (√x – 1) / ((√x – 1)(√x + 1)) → (√x + 1) / (x – 1)
[qui per eliminare "√" abbiamo usato la trasformazione (a – b)(a + b) → a2 – b2 con a = √x e b = 1]
• Si tratta di manipolazioni che sono comode in particolari casi. Spesso sono utili le trasformazioni opposte. Ad es. se devo operare mentalmente può essermi comodo pensare 1/√3 come √3/3, che, se ricordo che √3 ≈ 1.73, posso approssimare a 1.8/3 = 0.6. Se invece uso una calcolatrice e devo calcolare √3/3 mi conviene, viceversa, pensare a 1/√3 in modo da usare solo tre tasti (3 
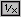 ).
).
• Quando si opera una razionalizzazione occorre controllare se si ottiene un termine equivalente o no.
Ad es. nel secondo degli esempi precedenti abbiamo operato anche la sostituzione di √x·√x con x che sono equivalenti solo per x ≥ 0;
in questo caso non vi sono problemi in quanto nel termine complessivo rimane presente un "√x" che impone la esclusione dal dominio degli x negativi.
Nel terzo esempio, invece, abbiamo ottenuto un termine che ha un dominio più ristretto rispetto a quello originale: non è definito per x = 1.
 Storia.
Storia.
|
1.
Mentre gli antichi Babilonesi (vedi) già nel 1800 a.C. non avevano alcuna preoccupazione a rappresentare numeri con più
cifre, comunque queste si susseguissero, i Greci, molti secoli dopo, non possedevano la scrittura posizionale dei numeri ed erano
convinti che ogni grandezza potesse essere espressa come il rapporto tra due numeri interi, ossia come numero razionale.
Non avevano, per esempio, idea che un numero che al quadrato facesse 2 doveva per forza essere irrazionale. Furono quindi scioccati quando
un discepolo di Piatgora scoprì che nel pentagrammma (stella a 5 punte), il loro simbolo di riconoscimento, il rapporto tra le lunghezze dei segmenti
A e B (vedi la figura a destra) non poteva essere espresso con un numero razionale (oggi sappiamo esprimere questo numero, che inzia con
1.61803398874…, con tutte le che vogliamo; tale numero viene chiamato sezione aurea).
|  |
2.
Lo script a cui puoi accedere da qui automatizza il calcolo della approssimazione con
cui posso conoscere il risultato di una operazione effettuata su dati approssimati. In modo analogo posso procedere con R
impiegando comandi come i seguenti, riferiti al calcolo di 3.14159265.../1.233444555...:
x1 <- 3.1; x2 <- 3.2; y1 <- 1.2; y2 <- 1.3
op <- c(x1/y1,x1/y2,x2/y1,x2/y2); print(c(min(op),max(op)),15)
# 2.38461538461538 2.66666666666667
x1 <- 3.14; x2 <- 3.15; y1 <- 1.23; y2 <- 1.24
op <- c(x1/y1,x1/y2,x2/y1,x2/y2); min(op);max(op)
# 2.53225806451613 2.56097560975610
x1 <- 3.141; x2 <- 3.142; y1 <- 1.233; y2 <- 1.234
op <- c(x1/y1,x1/y2,x2/y1,x2/y2); min(op);max(op)
# 2.54538087520259 2.54825628548256
Posso concludere che il risultato sta in [2.38,2.67], anzi in [2.532,2.561], anzi in [2.5453,2.5483], ….
Andando avanti potrei determinare il risultato con la precisione che voglio, facendo eventualmente il calcolo a mano
invece che con R.
In questo modo posso calcolare il risultato di qualsiasi operazione tra numeri reali che
sappia eseguire sui numeri decimali finiti.
Questo è il modo in cui sono definite le operazioni tra numeri reali. Sui numeri potenzialmente illimitati
operavano già i babilonesi, circa 4000 anni fa, ma il modo in cui operare tra numeri illimitati qui descritto risale
essenzialmente a Cantor, che lo ha definito rigorosamente nel 1871.
Nota. I calcoli con R descritti in questa voce possono essere eseguti più
facilmente caricando un'appostita libreria, nel modo seguente:
source("http://macosa.dima.unige.it/r.R")
div(x,y) divisione tra interi tra x ed y con resto:
div(180+270, 360) dà 1 90 div(180+270, 360)[2] dà 90
divisori(68); primi(68)
1 2 4 17 34 68 2 2 17
approssima( c(3.141,3.142), c(1.233,1.234), "/")
[1] min [2] max Usa approssima2 per centro e raggio
[1] 2.545381 2.548256
approssima2( c(3.141,3.142), c(1.233,1.234), "/")
[1] centro [2] raggio Usa approssima per min e max
[1] 2.546818580 0.001437705
Esercizi: 
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Si parla di struttura
numerica quando congiuntamente a un insieme numerico
(numeri reali, numeri interi, numeri naturali, numeri periodici,
numeri decimali limitati, …) si considerano uno o
più oggetti matematici che stabiliscano dei collegamenti tra i
vari numeri.
Si parla di struttura
numerica quando congiuntamente a un insieme numerico
(numeri reali, numeri interi, numeri naturali, numeri periodici,
numeri decimali limitati, …) si considerano uno o
più oggetti matematici che stabiliscano dei collegamenti tra i
vari numeri.



 35 decimi + 24 decimi
35 decimi + 24 decimi  [2.4, 2.6],
[2.4, 2.6],

 o, in genere, il software (usando il simbolo "^") effettuano il calcolo
non seguendo direttamente questo procedimento, ma con un algoritmo più efficiente, così come usano un algortimo per la radice quadrata
più efficiente di quello con cui l'abbiamo definita.
o, in genere, il software (usando il simbolo "^") effettuano il calcolo
non seguendo direttamente questo procedimento, ma con un algoritmo più efficiente, così come usano un algortimo per la radice quadrata
più efficiente di quello con cui l'abbiamo definita.


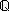 per indicare quello dei numeri razionali,
Z o
per indicare quello dei numeri razionali,
Z o 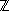 per quello degli interi ("z" è l'inziale della parola che in tedesco significa
"numero") e
N o
per quello degli interi ("z" è l'inziale della parola che in tedesco significa
"numero") e
N o  ,
, x3
x3
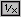 ).
).

