| • presentazione con esempi • difficoltà e misconcezioni da prevenire/affrontare • rapporti con altre discipline |
[Note di lavoro: al momento sono redatte in forma dettagliata solo le prime voci; potrebbe essere utile introdurre un link, oltre che al documento introduttivo/di inquadramento al nostro lavoro, anche ad una breve esplicitazione dell'impostazione della griglia, che metta in luce l'importanza di una introduzione "culturalmente significativa" dei concetti (ossia che sia riferimento per scelte successive - lavorative o di studio - consapevoli e sia percepita come un arricchimento culturale), l'importanza di riferimenti a "contesti" (per capire meglio natura e ruolo dei concetti, avere idea di come usarli per modellizzare situazioni e interpretare tali modellizzazioni, usarli come supporto per ragionamenti astratti, cogliere i collegamenti tra discipline), il ruolo delle attività di consolidamento tecnico e/o memorizzazione (quando sono utili e quando sono dannose, i rischi della dispersione concettuale, gli automatismi da apprendere esperienzialmente e gli atteggiamenti riflessivi da sviluppare), l'opportunità di rinviare ad eventuali studi successivi "formalizzazioni" non funzionali alla costruzione dei concetti o non motivate (ma mettere in luce, ed esemplificare e ragionare, sul ruolo della formalizzazione) e quella di raccordarsi con livelli scolastici precedenti (molte delle competenze/conoscenze indicate sono da "scuola di base"), l'importanza di porsi il problema di che cosa sia "obsoleto" (↔ provvisorietà anche di questa griglia), gli atteggiamenti trasversali importanti (argomentare, passare da un linguaggio all'altro, ricostruire/testare proprietà/metodi/... riferendosi ad esempi), ..., e illustri/faccia alcune proposte per l'uso di essa;]
| ||||||||||||
• Il simbolo 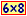 indica automatismi (di elaborazione, associazione, passaggio da una rappresentazione a un'altra, ...)
che tutti devono saper esercitare senza sforzi mnemonici o riflessivi
(per liberare risorse mentali da dedicare ad aspetti più concettuali);
si tratta di poche abilità/atteggiamenti che è opportuno consolidare/mantenere allenati continuamente.
indica automatismi (di elaborazione, associazione, passaggio da una rappresentazione a un'altra, ...)
che tutti devono saper esercitare senza sforzi mnemonici o riflessivi
(per liberare risorse mentali da dedicare ad aspetti più concettuali);
si tratta di poche abilità/atteggiamenti che è opportuno consolidare/mantenere allenati continuamente.• [e] è un link ad esempi di attività od esercizi (per chiarire il tipo di padronanza o di interazioni indicate). • [q] è un link ad esiti di questionari e altre prove di valutazione. • Cliccando [estendi] ottieni una visualizzazione della sezione e degli esempi a cui rinviano i link. Alcuni esempi sono utilizzati in più sezioni. | ||||||||||||
| Area disciplinare | ||||||||||||
| contenuto/metodo | padronanza richiesta: saper ... | difficoltà/misconcezioni | interazioni disciplinari | |||||||||
| Numeri | ||||||||||||
| (1) Interpretazione "geometrica" dei numeri (e dei rapporti) e delle operazioni tra essi
[estendi] Nota. Su rapporti e percentuali vedi anche Formule. |
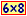 Interpretare immediatamente i numeri come posizioni sulla retta graduata [e] Interpretare immediatamente i numeri come posizioni sulla retta graduata [e]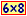 Associare immediatamente le frazioni più comuni a numeri minori di uno, a percentuali e
a rappresentazioni grafiche [e] Associare immediatamente le frazioni più comuni a numeri minori di uno, a percentuali e
a rappresentazioni grafiche [e]••• Usare queste associazioni per svolgere calcoli mentali [e] [e] ••• Usare queste associazioni e "cambi" per svolgere calcoli con percentuali e tempi [e] [e] 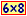 Interpretare immediatamente addizioni, Interpretare immediatamente addizioni, ••• Appoggiarsi a queste interpretazioni quando si opera con numeri negativi [e] ••• Appoggiarsi a interpretazioni "geometriche" anche per l'uso / il controllo di proprietà dei numeri reali [e] ••• Saper stimare rapporti tra grandezze rappresentate graficamente mediante superfici e volumi, saper confrontare (immaginando mentalmente quante volte una unità sta nell'altra) diverse unità di superficie o di volume/capacità [e] [e] [e] |
• − x è spesso considerato negativo;
diffusi errori nell'operare coi numeri negativi. Sembra utile al superamento di tali difficoltà: consolidare
l'interpretazione vettoriale di numeri e operazioni (compresa la
negazione), non far usare il "+" davanti ai numeri positivi, scoraggiare l'uso di regolette come
"− per − fa +". [q] • Le percentuali vengono calcolate (o si tenta di farlo) con complessi procedimenti invece che con una semplice divisione, e le parti che stanno in una certo rapporto col totale con altri procedimenti ad hoc invece che con una semplice moltiplicazione [q] [q] • Sono diffuse, più in generale, difficoltà ad operare con rapporti tra grandezze e a gestire le relazioni tra i rapporti di lunghezze e quelli di aree e di volumi (a cui si connettono difficoltà nella padronanza nei cambi di unità di misura di aree e volumi/capacità) [q] [q] • Difficoltà nell'operare con grandezze espresse in basi non decimali (si cerca di ricordare "regole" di calcolo invece di ricorrere a semplici cambi o appoggiarsi mentalmente a linee o cerchi graduati con scale non decimali) [q] |
• Evidentemente l'operare su numeri, variazioni, ... in contesti scientifici ed economici
favorisce la padronanza numerica, a patto che nell'insegnamento di tali ambiti disciplinari (specie nelle
materie socio-economiche) non si privilegi il
ricorso a disparati artifici di calcolo invece che ai concetti e alle tecniche essenziali (a volte si fanno
studiare formule e le loro "formule inverse", o affrontare
problemi di proporzionalità con regolette ad hoc per le "proporzioni" invece che
usando i concetti di base,
quali la relazione tra moltiplicazione e divisione, che entrano in gioco nella risoluzione delle equazioni).
Sarebbe, anzi, opportuno
coordinare gli insegnamenti delle diverse discipline in modo da condividere esempi, metodi, ... che
stimolino gli studenti a mettere in comunicazione mentalmente i diversi apprendimenti. [e] [e] [e] [e] |
|||||||||
| (2) Approssimazioni, calcoli mentali, potenze a esponente intero, unità di misura, uso delle calcolatrici
[estendi] |
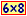 Interpretare come prodotti/divisioni le variazioni dell'esponente intero di una potenza
[e] Interpretare come prodotti/divisioni le variazioni dell'esponente intero di una potenza
[e]••• Associare le proprietà delle potenze a tale interpretazione 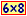 Esprimere l'ordine di grandezza di un numero a parole, esprimere un numero in notazione scientifica
[e] Esprimere l'ordine di grandezza di un numero a parole, esprimere un numero in notazione scientifica
[e]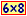 Troncare e arrotondare un numero
[e] Troncare e arrotondare un numero
[e]••• Utilizzare quanto elencato sopra per svolgere calcoli mentali approssimati [e] [e] 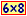 Rappresentare le approssimazioni come intervalli e come disequazioni
[e] Rappresentare le approssimazioni come intervalli e come disequazioni
[e]••• Utilizzare quanto elencato sopra per svolgere semplici calcoli con valori approssimati [e] [e] ••• Rendersi conto di quante possono essere le cifre significative del risultato di un calcolo tenendo conto del contesto, delle informazioni di cui si dispone, … [e] ••• Essere consapevoli della "astrattezza" del concetto di numero reale (e di retta) e dell'utilità che ne deriva per semplificare le attività di modellizzazione (oltre che di come di ciò si deve tener conto nell'usare nella pratica le modellizzazioni matematiche) [e] ([e]) ••• Essere consapevoli che numeri ed operazioni di una calcolatrice non soddisfano tutte le proprietà della struttura dei numeri reali [e] [e] |
• Le proprietà delle potenze vengono spesso memorizzate senza coglierne il significato e usate a sproposito o confondendole, senza saperle ricostruire o controllare • Non viene controllata la sensatezza dell'ordine di grandezza e della precisione dei risultati. [q] • Non ci si rende conto di come si opera con valori approssimati (e, quindi, non si ha neanche idea di come si opera con i numeri reali) [q] • Non ci si rende conto che, in un problema reale o realistico le informazioni numeriche di cui si dispone sono, in genere, approssimate. [q] • Di fronte a una sequenza di calcoli si approssimano i risultati intermedi e si opera su queste approssimazioni per ottenere il risultato finale invece che approssimare solo alla fine. (↔ imparare a usare la "memoria" delle calcolatrici) • Di fronte a un problema di calcolo non si è in grado di fare stime senza ricorrere a calcoli a mano o all'uso della calcolatrice, non si è in grado di fare controlli mentali dei risultati di una calcolatrice e rendersi conto degli eventuali errori di battitura, a utilizzare informazioni numeriche di cui si dispone per ricavarne altre, …: l'addestramento alla meccanicità scoraggia l'esercizio di ragionamenti di controllo, esplorazione, ... (specie nei ragazzi più "deboli") [q] |
• L'uso di approssimazioni e potenze di 10 è diffuso in tutte le discipline tecnico-scientifiche e
socio-economiche. Anche in esse si deve puntare, soprattutto nei primi anni,
alla padronanza del calcolo approssimato attraverso disequazioni piuttosto che con regolette "magiche" (ad es.
per il prodotto tra numeri positivi approssimati basta prendere l'intervallo delimitato dai prodotti delle approssimazioni per difetto ed eccesso).
È importante sottolineare che le percentuali sono in genere approssimate e
si deve tenerne conto passando ai valori assoluti o calcolando distribuzioni percentuali (ad es. l'ultima frequenza percentuale è bene non ricavarla per complemento a 100).
[e] [e] [e] [e] |
|||||||||
| (3) Operazioni tra numeri reali, concetto di numero razionale
[estendi] |
••• Sapere che la divisione tra due interi
genera un numero reale periodico e saper individuare il periodo eseguendo la divisione
[e] ••• Sapere che ogni numero periodico è esprimibile in modo finito anche come rapporto tra due interi, e saper trovare (senza aver memorizzato complessi procedimenti meccanici) due di tali interi [e] [e] ••• Saper sfruttare quanto sopra per svolgere particolari calcoli tra numeri periodici [e] ••• Sapere che cos'è (e che esiste, ovvero si può generare) la radice n-esima di un numero reale [e] ••• Avere l'idea, connessa al calcolo approssimato, di come le "quattro operazioni" e l'elevamento a potenza tra numeri decimali limitati possono essere estesi ai numeri reali [e] 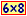 Saper collocare sulla linea dei numeri e/o stimare in forma decimale il valore di semplici
rappresentazioni simboliche (radici, 2π, …). Saper collocare sulla linea dei numeri e/o stimare in forma decimale il valore di semplici
rappresentazioni simboliche (radici, 2π, …).
|
• di fronte a un calcolo come • la grave misconcezione secondo la quale i numeri reali sono definiti come l'unione dei numeri razionali e dei numeri irrazionali, che spesso si intreccia alla confusione con altri significati del termine "irrazionale" (misconcezioni favorite da pratiche didattiche in cui i numeri reali, invece che introdotti come numeri decimali illimitati, sono presentati con "caricature", errate o non alla portata degli alunni, del "completamento" di Q) [q] [q] |
• la riflessione sui numeri come concetti/modelli matematici "astratti" si presta a svariati collegamenti con Filosofia e Fisica (Perché i Pitagorici sono andati in crisi
per la scoperta dell'esistenza di numeri non razionali? Esitono grandezze continue?
Le varie concezioni della natura "atomica" della materia. Le costanti fisiche dal valore definito "esattamente" - ε0, μ0, Z0, c - e quelle "misurate". ...)
[e] [e] [e] |
|||||||||
| (4) Altre rappresentazioni dei numeri [estendi] |
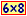 saper esprimere in base dieci un numero naturale espresso in base 2,
sapere che K indica una moltiplicazione per 210 = 1024 (non per 1000, come k), ...
[e]
saper esprimere in base dieci un numero naturale espresso in base 2,
sapere che K indica una moltiplicazione per 210 = 1024 (non per 1000, come k), ...
[e]••• saper trovare, mediante tentativi ragionati e approssimazioni successive, l'espressione in base 2 di un numero naturale espresso in base dieci [e] ••• saper che i numeri limitati in base dieci possono non esserlo in base 2 (e che questo può essere all'origine di problemi di interpretazione delle uscite di un programma - ad es. un foglio elettronico può visualizzare un numero intero ma avere internamente un numero che non lo è) [e] ••• saper che i numeri illimitati in base dieci possono non esserlo in base 60 (i tempi in ore 5.333… e 5.0333… diventano 5:20 e 5:02) ••• saper operare - usando metodi generali, non "regolette" - con espressioni temporali espresse con rappresentazioni miste (basi 10, 60, 12, 24 e 100); vedi quanto osservato al punto 1 del tema Numeri [e] ••• "aritmetica delle direzioni" ("aritmetica circolare" in [0,360): concetto di "=" in tale contesto; riduzione a [0,360) di un numero qualunque, ...) |
• errori nei calcoli coi tempi (vedi commenti sopra, al punto 1 del tema Numeri) • difficoltà legate sia al significato delle operazioni che alla padronanza dei significati "lessicografico" e "polinomiale" della scrittura posizionale • difficoltà legate al concetto di "resto", alla padronanza dell'equivalenza tra "A diviso B fa C con resto R" e A=B·C+R, e A/B=C+R/B (da collegare ad altri ambiti in cui interviene il concetto di resto) [q] |
• valgono considerazioni analoghe a quelle svolte nel punto 1 del tema Numeri.
Si tengano, poi, presenti: • i molteplici riferimenti a misure o codifiche di informazioni espresse in forma binaria presenti nei più disparati impieghi di sussidi elettronici [e] • i problemi legati all'uso dei fogli elettronici (e, in particolare, ai formati delle celle), diffuso in molte discipline, all'interno della promozione di un uso consapevole del software (essere consci dei limiti, della diversità tra ciò che "si vede" e ciò che c'è "dentro", …, motivare riflessioni disciplinari per comprendere il funzionamento). |
|||||||||
| Funzioni | ||||||||||||
| concetto di funzione In costruzione |
• modi diversi
(black-box, tabelle, formule, diagrammi di flusso, algoritmi, descrizione verbale, grafici, …)
di rappresentare funzioni, e in contesti diversi (fisici, economici, sociali, tecnologici, …),
e a seconda delle informazioni che ho, della tipologia delle "grandezze", delle esigenze di comunicazione, ...
[mettere esempi] • funzioni con diverse specifiche di input/output (tra numeri o altri oggetti, a 1 o più argomenti, ...) [mettere esempi] [e] • associare funzioni (descritte graficamente o ...) a fenomeni e/o a descrizioni verbali [e] [e] • saper associare Input ad Output, e Output a Input, a partire dalla lettura dei grafici [e] • saper specificare (a seconda dei casi) variabili di input e di output, parametri/costanti, senza rimanere legati ad associazioni stereotipate lettere-ruoli [mettere anche in 3ª colonna] • relazioni che non sono funzioni (consolidare con molti esercizi grafici) [e] (e con riferimenti a contesti) [e] • saper comporre/scomporre funzioni (sia descritte mediante formule che con tabelle o grafi) [↔ formule] [e] [e] • dominio • misconcetto per cui le funzioni siano solo quelle R → R |
|||||||||||
| le funzioni nei software In costruzione |
• calcolatrice, • foglio di calcolo, • applicazioni per disegno, • linguaggi di prog. [in difficoltà: padronanza di convenzioni non coerenti usate in analisi, utilità del software da questo punto di vista; difficoltà del tasto [f-1], ...] |
|||||||||||
| proprietà di funzioni numeriche a 1 input e 1 output e loro interpretazione grafica In costruzione |
•
iniettività, invertibilità (consolidare con molti esercizi grafici;
consolidare esempi di riferimento
utili da richiamare alla mente per mettere a fuoco alcuni problemi chiave.) • crescenza/decrescenza [e] [• difficoltà: a volte alunni usano "sale"/"scende" percorrendo il grafico da destra a sinistra; importanza della "metafora temporale"] • periodicita', saper ricavare il periodo dal grafico [e] [• saper distinguere fenomeni oscillatori da fenomeni periodici; consapevolezza degli usi diversi degli stessi termini presenti nelle scienze e nelle tecniche, in cui si usano frequenza e periodo anche per fenomeni oscillatori non periodici (con ampiezza variabile o neanche con periodicità del passaggio per la "posizione di riposo" - si parla di "frequenza variabile") [e]] • immagine/controimmagine di un insieme (e in particolare di un intervallo) mediante una funzione (collegamenti con propagazione errori, risoluzione di disequazioni, ...; esempi di misconcetti diffusi, legati a casi in cui la funzione a cambi di crescenza; evitare uso di "codominio" di F al posto di "immagine" o "insieme di variabilità" di F) [e] [e] [e] • avere mentalmente consolidati esempi chiave (qui un esempio che è utile richiamare in molte occasioni: valore assoluto, funzione inversa, dominio, risoluzione di equazioni e disequazioni, ...) |
|||||||||||
| particolari funzioni numeriche a 1 input e 1 output In costruzione |
•
rappresentazione analitica e grafica di: x  ax+b (automatismi), x ax+b (automatismi), x  x2, x x2, x  x3, x x3, x  1/x,
x 1/x,
x  |x| |x|• saper esemplificare/associare fenomeni a x → 1/x, x → x2, x → x3,... • composizione di funzioni e composizione di percentuali [x → x·(1+p/100), "diminuire del 10%" = "moltiplicare per 0.9", ...]; evidenziare vari misconcetti diffusi (e opportunità di renderne consapevoli gli alunni) • rappresentazione analitica e grafica di: x  sin(x), x sin(x), x  cos(x),
x cos(x),
x  ax, x ax, x  log(x) log(x)• rappresentazione analitica di funzioni che hanno i grafici delle precedenti trasformati mediante traslazioni, ribaltamenti, trasformazioni di scala; aver idea che cerchio di centro ... e raggio ..., retta di pendenza ... passante per ..., parabola di coefficiente direttivo ... con vertice in ... si ottengono dalle formule dei "grafici base" tutte allo stesso modo; saper eseguire la divisione con resto di due (ax+b)/(cx+d) e usarla per tracciare y = (ax+b)/(cx+d); • nelle difficoltà: x → f(x+h) è traslato di x → x-h, x → f(x·h) è scalato orizzontalmente di x → x/h; essere consapevoli [esserlo diventati attraverso opportuni "conflitti" da costruire nell'insegnamento] dei casi in cui il collegamento tra trasf. geom. e cambiamento di formula non è banale, in modo da allertarsi - come di fronte ai "cambiamenti di ora legale-solare" |
|||||||||||
| "idea consolidata" dei concetti base di analisi In costruzione |
•
distinguere funzioni continue e non; non confondere discontinuità con non definizione (per molti
alunni che arrivano all'università x → 1/x non
è continua!) • saper usare il simbolo/concetto di limite per rappresentare situazioni e fenomeni in contesti diversi • associare/controllare andamenti grafici e limiti, saper fare esempi (graficamente) di funzioni crescenti superiormente limitate, di funzioni crescenti definite su un intervallo superiormente limitato, ... [↔ misconcetti] • saper congetturare sperimentalmente limiti di funzioni (e successioni) (es) • saper individuare casi semplici di trascurabilità di un infinito/infinitesimo rispetto ad un altro • saper descrivere verbalmente e graficamente l'andamento della pendenza del grafico di una funzione • y = sin(x) per x vicino a 0 si comporta come y = x, y = exp(x) ... (e capacità di congetturare/ricostruire i limiti per x → 0 di sin(x)/x, • saper tracciare (a mano, e con una certa cura) i grafici di alcune funzioni base usando loro proprietà caratteristiche (se il sistema è monometrico y=sin(x) taglia l'origine con lo stesso andamento di y=x, e a destra sta sotto, a sinistra sopra di essa; y=exp(x) incontra la retta y=x+1 sull'asse y e altrove sta sopra di essa, ...) |
|||||||||||
| [COLLEGAMENTI: scienze sperimentali (funzioni, proprietà, associazione di andamenti a fenomeni, motivazioni, infinitesimi-termini trascurabili, funzioni approssimanti, ...); disegno(funzioni in software);] | ||||||||||||
| Formule | ||||||||||||
| ruolo, uso e struttura In costruzione |
• modellizzare situazioni, rappresentare proprietà, ... usando variabili,
[e]
[e]
[e]
[e]
• padronanza della struttura di termini e formule e di • modi per rappresentarla [e] [e] [e] [e] | |||||||||||
| manipolazioni di base In costruzione |
• dominio di termini e formule, problemi relativi (esprimere una variabile in funzione di altre, "valore" di termini e di formule, risolvere rispetto a ..., incognita, parametro, costante, ..., equivalenza algebrica)
(attenzioni generali
idee unificanti
idee unificanti)
• manipolazioni simboliche di base (espandere, fattorizzare, sostituire sottotermini) • imparare a richiamare semplici esempi per ricostruire certe formule, procedimenti, ... • sostituire sottotermini con variabili per ricondursi a manipolazioni più semplici (es.vari) [fa il paio con "studiare una funzione riconducendosi a grafici di funzioni base"] • argomentare/esplicitare i passaggi (vedi) [INVERTIRE formule, non memorizzare formule inverse; discorso ("duro"), in relazione a questo, sul rapporto con le altre displine; anche in relazione alle PROPORZIONI e alle PERCENTUALI, da NON manipolare con regolette ad hoc] |
|||||||||||
| interpretazioni grafiche In costruzione |
• saper intrecciare metodi/linguaggi grafici ed algebrici ... [↔ prop. numeri e funzioni: soluz. equaz. e disequaz., e sistemi]
[e]
• saper tradurre in formule trigonometriche simmetrie sul cerchio goniometrico [esempi vari di difficolta' degli alunni e considerazioni su ruolo di insegnamento nell'origine di esse] |
|||||||||||
| manipolazioni specifiche In costruzione |
• proprieta' delle potenze
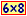 Saper usare le proprietà delle potenze per svolgere calcoli che coinvolgono radici
[e] (non radicali come cosa a se') Saper usare le proprietà delle potenze per svolgere calcoli che coinvolgono radici
[e] (non radicali come cosa a se')
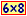 Saper confrontare termini frazionari usando le proprietà dei rapporti
[e] Saper confrontare termini frazionari usando le proprietà dei rapporti
[e]
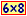 Saper sviluppare o semplificare
calcoli tra termini frazionari usando le proprietà dei rapporti e la prop. distributiva
[e] Saper sviluppare o semplificare
calcoli tra termini frazionari usando le proprietà dei rapporti e la prop. distributiva
[e]
• dividere polinomi, teorema del resto • combinare righe per risolvere sistemi lineari [NO Cramer (se non come corollario in un contesto più generale di algebra lineare)] [e] [• saper "usare" formule trigonometriche di addizione] • proprieta' di base di log ed exp • proprieta' delle varie funzioni (dove sono iniettive, dove crescono/decrescono, ...) che intervengono in una equazione/disequazione che deve essere risolta rispetto a una certa variabile e usarle integrandole ai metodi generali di risoluzione [misconcetti/difficoltà/problemi didattici: tante ricette per tanti tipi di equazioni, invece che le due o tre idee generali che servono, e che devono essere consolidate/ricontestualizzate/...] |
|||||||||||
| formule e software In costruzione |
• sintassi / semantica
• saper implementare semplici algoritmi con qualche software • idea/esperienza che, oltre alla calcolatrici, esistono strumenti di calcolo simbolico (e che, come per le calcolatrici, occorrono conoscenze adeguate per usarli bene) |
|||||||||||
| Statistica e Probabilità | ||||||||||||
| statistica descrittiva In costruzione |
• data una tabella di dati in un certo contesto scegliere il tipo di rappresentazione grafica piu' adatta [pensare ai disastri connessi all'uso dei FOGLI di calcolo]
(es)
• uso di unità e scale appropriate, "lettura" dei grafici, e alcuni degli altri aspetti che avevamo considerati nella scaletta comune matematica-scienze (vedi) • media, mediana, percentili, classi modali e loro interpretazione geometrico/grafica • numeri indici, distribuzione, frequenza relativa, densita' di frequenza • problemi (di calcolo e di rappresentazione grafica) connessi al tipo di informazioni (dati singoli, dati classificati, dati approssimati, ...) • "idea" del problema del campionamento |
|||||||||||
| approssimare fenomeni variabili a partire dalla conoscenza di dati sperimentali In costruzione |
• valutare la compatibilita' tra rilevamenti sperimentali e modelli matematici, valutare parametri, ... (punti-rettangolini, cuva per essi, ...)
(es)
• approssimazione e interpolazione (lineare) • ... |
|||||||||||
| le misure di probabilità In costruzione |
• probabilita' come "misura" a valori in [0,1]
• idea di variabile casuale (↔ variabile deterministica) e di fenomeno ed evento casuale (↔ carenza di informazioni) • come dare una legge di distribuzione nel caso discreto e nel caso continuo • distribuzione uniforme, "esempi" di distribuzioni non uniformi • saper usare le proprieta' delle misure per semplici calcoli probabilistici (nel caso discreto e nel caso continuo) • probabilita' condizionata (e sue rappresentazioni con grafi e tabelle di contingenza); • semplici esempi di calcoli probabilistici usando concetti di calcolo combinatorio |
|||||||||||
| avvio alla statistica inferenziale In costruzione |
• estensione dei concetti statistici di media e mediana a quelli probabilisitici
(da istogramma sperimentale e istogramma teorico), collegamenti col tema "misura e variazioni"
(integrale ↔ misura di probabilita')
• idea di (teorema limite centrale e) intervallo di confidenza (da un'indagine campionaria non posso stabilire con certezza che un certo fenomeno sull'intera popolazione misuri A±ε, ma solo con una certa probabilità, interdipendente da ε) • saper fare semplici simulazioni (da RND a ...) |
|||||||||||
| Geometria | ||||||||||||
In costruzione |
• figure "ideali" di base (punto, retta, semipiano, ...) e
proprieta' e relazioni principali (ordinamento, densita', distanza, ...) e
loro rappresentazione matematica (numero reale, equazione, ...)
• principali proprietà/teoremi su rette, cerchi, triangoli (...) nel piano euclideo [cioè quello in cui vale la metrica euclidea e ..., comunque lo si sia introdotto] - saper usare [6×8] t. Pitagora, similitudini (proiezioni parallele), somma angoli triangoli, direzioni/angoli (due rette che intersecano una terza retta formando con essa [rispetto a una sua fissata direzione] angoli uguali sono parallele), ... [mettere esempi d'uso] - triangolo in semicerchio, centro di un cerchio come intersezione ASSI - elementi nec./suff. per individuare un triangolo/cerchio - collegamento con tecniche di disegno (compasso, software grafico, software analitico, ...) • intrecciare metodi sintetici e analitici per definire, dimostrare, risolvere problemi, costruire figure (anche col COMPUTER) (... luoghi ...) • saper esplorare (mentalmente) dinamicamente le proprieta' di una figura (casi limite, che cosa si conserva, al cambiare di una cosa quale altra cambia e come, ...; anche usando (semplice) software), far congetture a partir da esempi, ideare controesempi, interpretare geometricamente/matematicamente movimenti di oggetti, macchinari, ..., associare caratteristiche fisiche (statiche, dinamiche, ...) a caratteristiche geometriche, ... • saper descrivere analiticamente alcune trasformazioni i geometriche (traslazioni, simmetrie rispetto assi, trasformazioni di scala, rotazioni di multipli di 90 gradi) • avere idea delle trasformazioni affini e proiettive come proiezioni parallele e centrali tra piani (e invarianze) • coordinate cartesiane e polari [coordinate polari: operativamente, e non formulette a memoria] • vettori e versori in forma cartesiana e polare, interpretazione geometrica di prodotti scalare e vettoriale • coordinate tridimensionali, vettori tridimensionali, curve di livello • geometria come "modello" di spazio, non come "spazio vero" [COLLEGAMENTI: fisica (cinematica, vettori, ...), geografia astronomica, disegno/arte, filosofia, ...] |
|||||||||||
| Matematica finita | ||||||||||||
In costruzione |
• saper modellizzare graficamente (grafi, "pallini", ...) problemi combinatori e/o di scelte successive
e utilizzare le rappresentazioni per risolvere semplici problemi e/o costruire formule
• saper associare il fattoriale a qualche fenomeno modellizzabile con esso • aver idea di che cosa C(n,k) e che puo' essere calcolato in piu' modi (e saper leggere e usare uno di questi metodi di calcolo) • idea della esplosione combinatoria (es. aver visto la modellizzazione di almeno un esempio, ad es. quanti insiemi si possono formare con N oggetti, e avere idea di collegamenti con la "complessita'" / la "non rarita'" / ... di altri fenomeni [importanza educativa generale]) • definizioni ricorsive (saperle "usare" per calcolare valori) e qualche esempio di loro implementazioni informatiche (i "cicli", il "compila" di un foglio elettronico, la battitura ripetuta di tasti di una calcolatrice, ...) [• non è importante ricordare formule ma aver visto prototipi di modellizzazione matematica e risoluzione di problemi di tipo combinatorio (e non essere "smarriti" di fronte a un problema del genere) [COLLEGAMENTI: informatica, fisica, chimica, scienze sociali] |
|||||||||||
| Misure e variazioni | ||||||||||||
| ↔ funzioni, statistica, geometria
In costruzione |
• variazione assoluta, variazione relativa, pendenza, ...
• avere l'idea di come il concetto di limite permette di determinare la pendenza del grafico di una funzione in un punto; saper calcolare la derivata delle funzioni polinomiali; sapere che le funzioni esponenziali sono proporzionali alla loro pendenza (e che hanno "tempi di raddoppiamento" [o dimezzamento o di moltiplicazione per k] costanti, riferendolo a fenomeni biologici e/o economici e/o fisici e/o combinatori) [• importanza di ciò anche in relazione al misconcetto, diffuso e interiorizzato - e a volte generato dall'insegnamento di altre discipline-, che confonde crescenza con diretta proporzionalità] • saper usare il simbolo/concetto di derivata per rappresentare la rapidità di variazione di fenomeni in contesti diversi • semplici problemi di min/max graficamente e analiticamente (es) • semplici modelli differenziali (P(0) = p0, P(n+1) = P(n)*k, deposito in manca, cinematica, legge raffreddamento di Newton, ...): costruzione ed eventuale esplicitazione [a livello elementare, quel che è necessario per capire "qualcosa" di fisica, economia, biologia, ..., riuscire a razionalizzare il funzionamento di automatismi] • angolo come lunghezza d'arco (idea di come misurare "matematicamente" un angolo/arco per approssimazioni successive - radianti - grado [°] come abbreviazione di π/180) (es) [misconcetti: sin(1) confuso con sin(1°), ...] • idea di integrazione (definita) per misurare lunghezze (es), aree (es) e volumi [COLLEGAMENTI: fisica, economia, ...] |
|||||||||||
| Che cos'è la Matematica? | ||||||||||||
| Riflessioni sulla sua natura e i suoi metodi
In costruzione |
• "qualche" esplorazione di oggetti matematici lontani dalla "intuizione sensibile" ma frutto di modellizzioni interne alla matematica, e loro successive applicazioni (es-: "gruppo", "numero complesso" [es], "infinito attuale", "geometrie strane" [altri spazi], ...)
• "qualche" esplorazione dell'evoluzione di argomenti classici (es.: matrici-algebra lineare e sue svariate applicazioni [es.uso], dai grafici di funzioni alle "curve" o alle superfici, dall'algoritmo alla "definizione" di computer, ...) • "qualche" esplorazione della matematica "incorporata" nelle cose • modi in cui si possono dare le definizioni di oggetti matematici (costruzione o "assiomi" che caratterizzano come usarli) • linguaggio comune, linguaggio matematico e altri linguaggi specialistici ... • ripresa "a spirale" dei concetti; concreto → astratto → concreto → astratto → ... [collegamenti con Filosofia e Fisica; "modello" ↔ "idee" di Platone (caverna, Menone);...] [e] |
|||||||||||
| Aspetti TRASVERSALI [da vedere se collocare qui]
eventualmente spezzabile in due: "Modellizzazione e problem solving" e "Metodi, strategie, atteggiamenti trasversali" | ||||||||||||
| In costruzione |
• mettere i più significativi aspetti presenti nelle varie voci • non vuol dire sapere tutto (ma costruire basi per eventuali conoscenze piu' formalizzate dopo: non brutta copia dell'università,...) |
|||||||||||
| XXX | |||